搜索
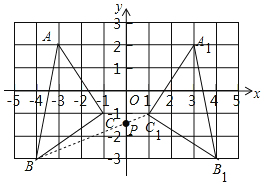
【题目】如图，在平面直角坐标系中，A(-3,2)，B(-4,-3)，C(-1,-1)．
(1)①在图中作出△ABC 关于y轴对称的△A1B1C1并写出点C1 的坐标（直接写答案）：C1______；②△A1B1C1 的面积为______．
(2)在y轴上画出点 P，使 PB+PC 最小．
参考答案：
【答案】（1）①作图见解析，C1（1，-1）；②
；（2）见解析.
【解析】
（1）①分别作出点A、B、C关于y轴的对称点A1、B1、C1，连接即可，根据点C1的位置即可写出其坐标；
②利用分割法计算即可．
（2）连接BC1与y轴的交点即为所求的点P．
（1）①如图，△A1B1C1即为所求；由图象可知：C1（1，-1）；
②S=3×5-
×1×5-×2×3-×2×3=；
（2）如图，连接BC1与y轴的交点为P，点P即为所求．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=﹣
x2+（3m+1）x﹣m（m＞且为实数）与x轴分别交于点A、B（点B位于点A的右侧且AB≠OA），与y轴交于点C．
（1）填空：点B的坐标为 ，点C的坐标为 （用含m的代数式表示）；
（2）当m=3时，在直线BC上方的抛物线上有一点M，过M作x轴的垂线交直线BC于点N，求线段MN的最大值；
（3）在第四象限内是否存在点P，使得△PCO，△POA和△PAB中的任意两三角形都相似（全等是相似的特殊情况）？如果存在，请直接写出点P的坐标；如果不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知∠MON＝30°，点 A1,A2,A3…在射线ON 上，点B1,B2,B3…在射线OM 上，△A1B1A2，△A2B3A3，△A3B3A4
均为等边三角形，若OA1=2，则△A7B7A8 的边长为____.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，∠ACB=90°，AC=6cm，BC=8cm．点P从A点出发沿A→C→B路径向终点运动，终点为B点；点Q从B点出发沿B→C→A路径向终点运动，终点为A点．点P和Q分别以每秒1cm和3cm的运动速度同时开始运动，当一个点到达终点时另一个点也停止运动，在某时刻，分别过P和Q作PE⊥l于E，QF⊥l于F．设运动时间为t秒，则当t=______秒时，△PEC与△QFC全等．
-
科目： 来源： 题型：
查看答案和解析>>【题目】将一些完全相同的正三角形按如图所示规律摆放，第一个图形有1个正三角形，第二个图形有5个正三角形，第三个图形有12个正三角形，…，按此规律排列下去，第六个图形中正三角形的个数是（ ）
A. 35 B. 41 C. 45 D. 51
-
科目： 来源： 题型：
查看答案和解析>>【题目】我们知道“对称补缺”的思想是解决与轴对称图形有关的问题的一种重要的添加辅助线的策略，参考这种思想解决下列问题.
在△ABC中，D为△ABC外一点.
(1)如图1，若AC平分∠BAD,CE⊥AB于点E，∠ B+∠ADC=180,求证：BC=CD;
(2)如图2，若∠ACB=90°, AC=BC，F是AC上一点，AD⊥BF交BF延长线于点D，且BF是∠CBA的角平分线.求证：2AD=BF.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校数学兴趣小组进行户外兴趣活动：测量河中桥墩露出水面部分AB的高度．如图所示，在点C处测得∠BCA=45°．在坡比为i=1：3，高度DE=15米的小山坡顶E处测得桥墩顶部B的仰角为20°，则桥墩露出水面部分AB的高度约为（精确到1米，参考数据：sin20°≈0.34，cos20°≈0.94，tan20°≈0.36）（ ）
A. 34 B. 48 C. 49 D. 64
相关试题
