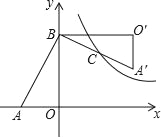
【题目】如图,在Rt△AOB中,直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,将△AOB绕点B逆时针旋转90°后,得到△A′O′B,且反比例函数y=![]() 的图象恰好经过斜边A′B的中点C,若SABO=4,tan∠BAO=2,则k=_____.
的图象恰好经过斜边A′B的中点C,若SABO=4,tan∠BAO=2,则k=_____.
参考答案:
【答案】6
【解析】设点C坐标为(x,y),作CD⊥BO′交边BO′于点D,
∵tan∠BAO=2,
∴![]() =2,
=2,
∵S△ABO=![]() AOBO=4,
AOBO=4,
∴AO=2,BO=4,
∵△ABO≌△A'O'B,
∴AO=A′O′=2,BO=BO′=4,
∵点C为斜边A′B的中点,CD⊥BO′,
∴CD=![]() A′O′=1,BD=
A′O′=1,BD=![]() BO′=2,
BO′=2,
∴x=BO﹣CD=4﹣1=3,y=BD=2,
∴k=x·y=3×2=6.
故答案为6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,定义:在直角三角形ABC中,锐角α的邻边与对边的比叫做角α的余切,记作ctanα,即ctanα=
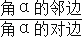 =
=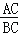 ,根据上述角的余切定义,解下列问题:
,根据上述角的余切定义,解下列问题:(1)如图1,若BC=3,AB=5,则ctanB= ;
(2)ctan60°= ;
(3)如图2,已知:△ABC中,∠B是锐角,ctan C=2,AB=10,BC=20,试求∠B的余弦cosB的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上,已知DE=0.5米,EF=0.25米,目测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=20米,求旗杆的高度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,⊙P的圆心是(2,a)(a >0),半径是2,与y轴相切于点C,直线y=x被⊙P截得的弦AB的长为
 ,则a的值是( )
,则a的值是( )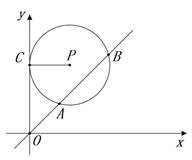
A.
 B.
B.  C.
C.  D.
D. 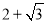
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,O是AC上一动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.若点O运动到AC的中点,则∠ACB=_____°时,四边形AECF是正方形.

-
科目: 来源: 题型:
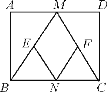
查看答案和解析>>【题目】如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是边BM,CM的中点,当AB与AD满足什么条件时,四边形MENF是正方形?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,边长为6,D是BC边上的动点,∠EDF=60°.
(1)求证:△BDE∽△CFD;
(2)当BD=1,CF=3时,求BE的长.

相关试题

