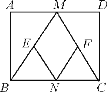
【题目】如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是边BM,CM的中点,当AB与AD满足什么条件时,四边形MENF是正方形?说明理由.
参考答案:
【答案】当AB∶AD=1∶2时,四边形MENF是正方形,理由见解析.
【解析】
当AB∶AD=1∶2时,AB=AM=DM=DC,求出∠BMC=90°,根据三角形中位线定理得到,NF∥BM,NE∥CM,结合ME=MF,∠BMC=90°,可得四边形MENF是正方形.
当AB∶AD=1∶2时,四边形MENF是正方形,
理由:∵AB∶AD=1∶2,AM=DM,AB=CD,
∴AB=AM=DM=DC,
∵∠A=∠D=90°,
∴∠ABM=∠AMB=∠DMC=∠DCM=45°,
∴∠BMC=90°,
∵四边形ABCD是矩形,
∴∠ABC=∠DCB=90°,
∴∠MBC=∠MCB=45°,
∴BM=CM,
∵N,E,F分别是BC,BM,CM的中点,
∴BE=CF,ME=MF,NF∥BM,NE∥CM,
∴四边形MENF是平行四边形,
∵ME=MF,∠BMC=90°,
∴四边形MENF是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,⊙P的圆心是(2,a)(a >0),半径是2,与y轴相切于点C,直线y=x被⊙P截得的弦AB的长为
 ,则a的值是( )
,则a的值是( )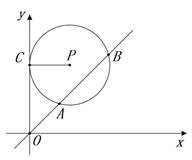
A.
 B.
B.  C.
C.  D.
D. 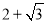
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△AOB中,直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,将△AOB绕点B逆时针旋转90°后,得到△A′O′B,且反比例函数y=
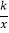 的图象恰好经过斜边A′B的中点C,若SABO=4,tan∠BAO=2,则k=_____.
的图象恰好经过斜边A′B的中点C,若SABO=4,tan∠BAO=2,则k=_____.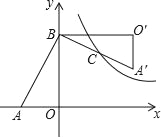
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,O是AC上一动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.若点O运动到AC的中点,则∠ACB=_____°时,四边形AECF是正方形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,边长为6,D是BC边上的动点,∠EDF=60°.
(1)求证:△BDE∽△CFD;
(2)当BD=1,CF=3时,求BE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装销售店到生产厂家选购A,B两种品牌的服装,若购进A品牌服装1套,B品牌服装1套,共需205元;若购进A品牌服装2套,B品牌服装3套,共需495元.
(1)求A,B两种品牌的服装每套进价分别为多少元?
(2)若A品牌服装每套售价为150元,B品牌服装每套售价为100元,根据市场的需求,现决定购进B品牌服装数量比A品牌服装数量的2倍还多3套.如果购进B品牌服装不多于47套,且服装全部售出后,获利总额不少于1245元,问共有哪几种进货方案?哪种进货方案获利最多?最多是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,点D是BC边的中点,BD=2,tanB=
 .
.(1)求AD和AB的长;
(2)求sin∠BAD的值.

相关试题

