【题目】如图1,定义:在直角三角形ABC中,锐角α的邻边与对边的比叫做角α的余切,记作ctanα,即ctanα=![]() =
=![]() ,根据上述角的余切定义,解下列问题:
,根据上述角的余切定义,解下列问题:
(1)如图1,若BC=3,AB=5,则ctanB= ;
(2)ctan60°= ;
(3)如图2,已知:△ABC中,∠B是锐角,ctan C=2,AB=10,BC=20,试求∠B的余弦cosB的值.

参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)先利用勾股定理计算出AC=4,然后根据余切的定义求解;
(2)根据余切的定义得到ctan60°=![]() ,然后把tan60°=
,然后把tan60°=![]() 代入计算即可;
代入计算即可;
(3)作AH⊥BC于H,如图2,先在Rt△ACH中利用余切的定义得到ctanC=![]() =2,则可设AH=x,CH=2x,BH=BC﹣CH=20﹣2x,接着再在Rt△ABH中利用勾股定理得到(20﹣2x)2+x2=102,解得x1=6,x2=10(舍去),所以BH=8,然后根据余弦的定义求解.
=2,则可设AH=x,CH=2x,BH=BC﹣CH=20﹣2x,接着再在Rt△ABH中利用勾股定理得到(20﹣2x)2+x2=102,解得x1=6,x2=10(舍去),所以BH=8,然后根据余弦的定义求解.
解:(1)∵BC=3,AB=5,
∴AC=![]() =4,
=4,
∴ctanB=![]() =
=![]() ;
;
(2)ctan60°=![]() =
=![]() =
=![]() ;
;
(3)作AH⊥BC于H,如图2,
在Rt△ACH中,ctanC=![]() =2,
=2,
设AH=x,则CH=2x,
∴BH=BC﹣CH=20﹣2x,
在Rt△ABH中,∵BH2+AH2=AB2,
∴(20﹣2x)2+x2=102,解得x1=6,x2=10(舍去),
∴BH=20﹣2×6=8,
∴cosB=![]() =
=![]() =
=![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】设AB,CD是⊙O的两条弦,AB∥CD,若⊙O半径为5,AB=8,CD=6,则AB与CD之间的距离为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】规定海平面的海拔高度为0米,珠穆朗玛峰高于海平面8844.43米,其海拔高度记作+8844.43米,那么吐鲁番盆地低于海平面155米,则其海拔高度记作( )
A. +155米 B. -155米 C. +8689.43米 D. -8689.43米
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF,△BEF的面积分别为S△ABC,S△ADF,S△BEF,且S△ABC=12,则S△ADF﹣S△BEF= .
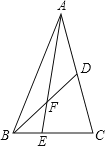
-
科目: 来源: 题型:
查看答案和解析>>【题目】求证:任意三角形的三个外角中至多有一个直角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,AB=AC=12厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为v厘米/秒,则当△BPD与△CQP全等时,v的值为( )
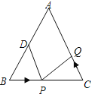
A. 2或3 B. 3 C. 2 D. 1或5
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x=a是方程x2+x﹣1=0的一个实数根,则代数式3a2+3a﹣5的值是__________.
相关试题

