【题目】如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E,F分别在BC和CD上,下列结论: ①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=2+ ![]() .
.
其中正确的序号是(把你认为正确的都填上).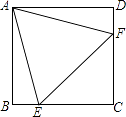
参考答案:
【答案】①②④
【解析】解:∵四边形ABCD是正方形, ∴AB=AD,
∵△AEF是等边三角形,
∴AE=AF,
在Rt△ABE和Rt△ADF中,![]() ,
,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,
∵BC=DC,
∴BC﹣BE=CD﹣DF,
∴CE=CF,
∴①说法正确;
∵CE=CF,
∴△ECF是等腰直角三角形,
∴∠CEF=45°,
∵∠AEF=60°,
∴∠AEB=75°,
∴②说法正确;
如图,连接AC,交EF于G点,
∴AC⊥EF,且AC平分EF,
∵∠CAF≠∠DAF,
∴DF≠FG,
∴BE+DF≠EF,
∴③说法错误;
∵EF=2,
∴CE=CF= ![]() ,
,
设正方形的边长为a,
在Rt△ADF中,
AD2+DF2=AF2 , 即a2+(a﹣ ![]() )2=4,
)2=4,
解得a= ![]() ,
,
则a2=2+ ![]() ,
,
S正方形ABCD=2+ ![]() ,
,
④说法正确,
所以答案是:①②④.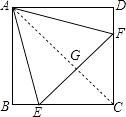
【考点精析】关于本题考查的等边三角形的性质和正方形的性质,需要了解等边三角形的三个角都相等并且每个角都是60°;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若△ABC∽△A′B′C′,相似比为1:2,则△ABC与△A′B′C′的面积的比为( )
A.1:2
B.2:1
C.1:4
D.4:1 -
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:2x3-8xy2=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在□ABCD中,∠A、∠B的度数之比为5∶4,则∠C等于( )
A. 60° B. 80° C. 100° D. 120°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A=3x2+3y2﹣5xy,B=2xy﹣3y2+4x2 .
(1)化简:2B﹣A;
(2)已知﹣a|x﹣2|b2与 aby的同类项,求2B﹣A的值.
aby的同类项,求2B﹣A的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
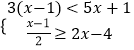 并求它的所有的非负整数解.
并求它的所有的非负整数解. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两同学的家与学校的距离均为3000米.甲同学先步行600米,然后乘公交车去学校、乙同学骑自行车去学校.已知甲步行速度是乙骑自行车速度的
 ,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家发去学校,结果甲同学比乙同学早到2分钟.
,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家发去学校,结果甲同学比乙同学早到2分钟.(1)求乙骑自行车的速度;
(2)当甲到达学校时,乙同学离学校还有多远?
相关试题

