【题目】某中学为开拓学生视野,开展“课外读书周”活动,活动后期随机调查了九年级部分学生一周的课外阅读时间,并将结果绘制成两幅不完整的统计图,请你根据统计图(图1)的信息回答下列问题:
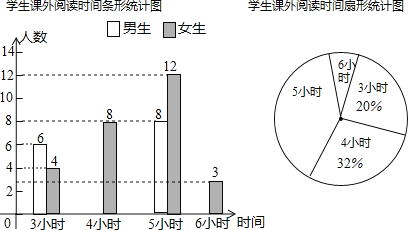
(1)本次调查的学生总数为________人,被调查学生的课外阅读时间的中位数是________小时,众数是_________小时;
(2)请你补全条形统计图,在扇形统计图中,课外阅读时间为![]() 小时的扇形的圆心角度数是_________;
小时的扇形的圆心角度数是_________;
(3)若全校九年级共有学生![]() 人,估计九年级一周课外阅读时间为
人,估计九年级一周课外阅读时间为![]() 小时的学生有多少人?
小时的学生有多少人?
(4)若学校选取![]() 、
、![]() 、
、![]() 、
、![]() 四人参加阅读比赛,两人一组分为两组,求
四人参加阅读比赛,两人一组分为两组,求![]() 与
与![]() 是一组的概率,(列表或树状图)
是一组的概率,(列表或树状图)
参考答案:
【答案】(1)50,4,5;(2)图见解析,144;(3)56人;(4)图表见解析,![]()
【解析】
(1)用阅读为3小时的人数除以它所占的百分比得到调查的总人数,根据中位数和众数的定义确定被调査学生的课外阅读时间的中位数和众数;
(2)先计算课外阅读时间为6小数的男生人数,再补全条形统计图;然后用出课外阅读时间为5小时的人数所占的百分比乘以![]() 得到扇形统计图中课外阅读时间为5小时的扇形的圆心角度数;
得到扇形统计图中课外阅读时间为5小时的扇形的圆心角度数;
(3)用700乘以样本中课外阅读时间为6小时的人数所占的百分比即可;
(4)画树状图展示所有12种等可能的结果数,找出![]() 与
与![]() 是一组的结果数,然后根据概率公式计算.
是一组的结果数,然后根据概率公式计算.
解:(1)![]() ,
,
所以本次调査的学生总数为50人;
被调査学生的课外阅读时间的中位数是4小时,众数是5小时;
(2)课外阅读时间为6小数的男生人数为![]() (人
(人![]()
补全条形统计图为:
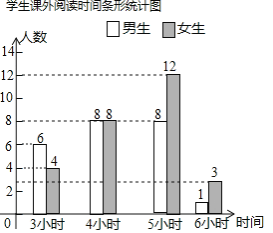
在扇形统计图中,课外阅读时间为5小时的扇形的圆心角度数![]() ,
,
故答案为50;4,5;![]() ;
;
(3)![]() ,
,
所以估计九年级一周课外阅读时间为6小时的学生有56人;
(4)画树状图为:
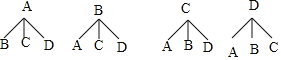
共有12种等可能的结果数,其中![]() 与
与![]() 是一组的结果数为4,
是一组的结果数为4,
所以![]() 与
与![]() 是一组的概率
是一组的概率![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点
 是菱形
是菱形 的
的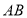 边上一点,点
边上一点,点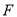 在
在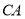 的延长线上
的延长线上(1)如图
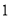 ,若
,若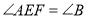 ,
,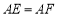 ,求
,求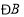 的度数;
的度数;(2)如图
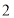 ,若
,若 是
是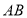 的中点,
的中点,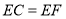 ,求
,求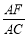 的值;
的值;(3)如图
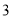 ,若
,若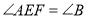 ,点
,点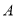 是线段
是线段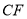 的中点,求证:
的中点,求证: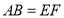

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在
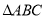 中,
中,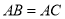 ,求作
,求作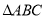 的外心
的外心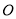 ,以下是甲、乙两同学的作法:对于两人的作法:
,以下是甲、乙两同学的作法:对于两人的作法:甲:如图1,(1)作
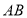 的垂直平分线
的垂直平分线 ;
;(2)作
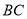 的垂直平分线
的垂直平分线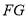 ;
;(3)
 ,
,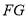 交于点
交于点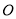 ,则点
,则点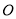 即为所求.
即为所求.乙:如图2,(1)作
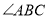 的平分线
的平分线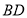 ;
;(2)作
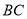 的垂直平分线
的垂直平分线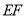 ;
;(3)
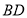 ,
,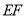 交于点
交于点 ,则点
,则点 即为所求.
即为所求.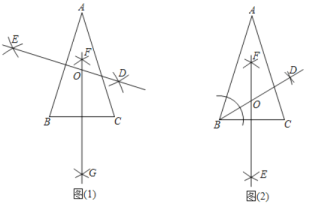
对于两人的作法,正确的是( )
A.两人都对B.两人都不对C.甲对,乙不对D.甲不对,乙对
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
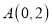 ,
,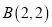 ,
,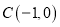 ,抛物线
,抛物线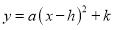 过点
过点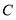 ,顶点
,顶点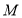 位于第一象限且在线段
位于第一象限且在线段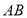 的垂直平分线上,若抛物线与线段
的垂直平分线上,若抛物线与线段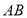 无公共点,则
无公共点,则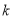 的取值范围是( )
的取值范围是( )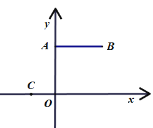
A.
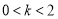 B.
B.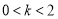 或
或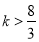 C.
C.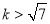 D.
D.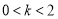 或
或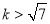
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点
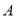 ,
,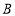 ,
,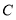 ,
,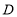 的坐标分别为
的坐标分别为 ,
,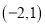 ,
, ,
, .线段
.线段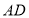 ,
,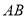 ,
,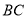 组成的图形为图形
组成的图形为图形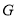 ,点
,点 沿
沿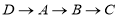 移动,设点
移动,设点 移动的距离为
移动的距离为 ,直线
,直线 过点
过点 ,且在点
,且在点 移动过程中,直线
移动过程中,直线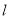 随
随 运动而运动.
运动而运动.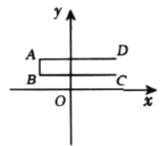
(1)若点
 过点
过点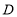 时,求直线
时,求直线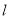 的解析式;
的解析式;(2)当
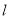 过点
过点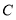 时,求
时,求 值;
值;(3)①若直线
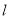 与图形
与图形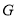 有一个交点,直接写出
有一个交点,直接写出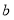 的取值范围;
的取值范围;②若直线
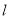 与图形
与图形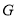 有两个交点,直接写出
有两个交点,直接写出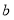 的取值范围.
的取值范围. -
科目: 来源: 题型:
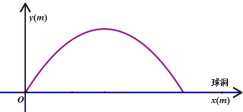
查看答案和解析>>【题目】在高尔夫球训练中,运动员在距球洞
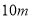 处击球,其飞行路线满足抛物线
处击球,其飞行路线满足抛物线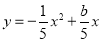 ,其图象如图所示,其中球飞行高度为
,其图象如图所示,其中球飞行高度为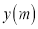 ,球飞行的水平距离为
,球飞行的水平距离为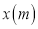 ,球落地时距球洞的水平距离为
,球落地时距球洞的水平距离为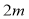 .
.
(1)求
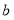 的值;
的值;(2)若运动员再一次从此处击球,要想让球飞行的最大高度不变且球刚好进洞,则球的飞行路线应满足怎样的抛物线,求抛物线的解析式;
(3)若球洞
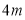 处有一横放的
处有一横放的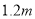 高的球网,球的飞行路线仍满足抛物线
高的球网,球的飞行路线仍满足抛物线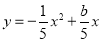 ,要使球越过球网,又不越过球洞(刚好进洞),求
,要使球越过球网,又不越过球洞(刚好进洞),求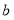 的取值范围.
的取值范围. -
科目: 来源: 题型:
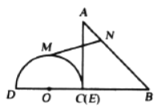
查看答案和解析>>【题目】如图,在
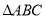 中,
中,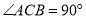 ,
,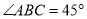 ,
,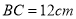 ,半圆
,半圆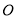 的直径
的直径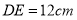 .点
.点 与点
与点 重合,半圆
重合,半圆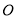 以
以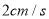 的速度从左向右移动,在运动过程中,点
的速度从左向右移动,在运动过程中,点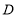 、
、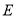 始终在
始终在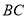 所在的直线上.设运动时间为
所在的直线上.设运动时间为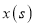 ,半圆
,半圆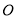 与
与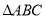 的重叠部分的面积为
的重叠部分的面积为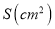 .
.
(1)当
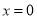 时,设点
时,设点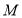 是半圆
是半圆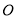 上一点,点
上一点,点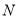 是线段
是线段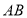 上一点,则
上一点,则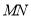 的最大值为_________;
的最大值为_________;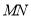 的最小值为________.
的最小值为________.(2)在平移过程中,当点
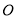 与
与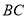 的中点重合时,求半圆
的中点重合时,求半圆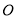 与
与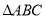 重叠部分的面积
重叠部分的面积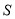 ;
;(3)当
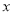 为何值时,半圆
为何值时,半圆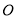 与
与 的边所在的直线相切?
的边所在的直线相切?
相关试题

