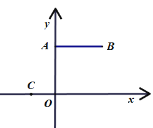
【题目】如图,已知![]() ,
,![]() ,
,![]() ,抛物线
,抛物线![]() 过点
过点![]() ,顶点
,顶点![]() 位于第一象限且在线段
位于第一象限且在线段![]() 的垂直平分线上,若抛物线与线段
的垂直平分线上,若抛物线与线段![]() 无公共点,则
无公共点,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() 或
或![]() C.
C.![]() D.
D.![]() 或
或![]()
参考答案:
【答案】B
【解析】
由点![]() 、
、![]() 的坐标结合抛物线
的坐标结合抛物线![]() 的顶点
的顶点![]() 位于第一象限且在线段
位于第一象限且在线段![]() 的垂直平分线上,即可得出
的垂直平分线上,即可得出![]() 值以及
值以及![]() ,分点
,分点![]() 在线段
在线段![]() 下方及点
下方及点![]() 在线段
在线段![]() 上方两种情况考虑抛物线与线段
上方两种情况考虑抛物线与线段![]() 无公共点,当点
无公共点,当点![]() 在线段
在线段![]() 下方时,根据点
下方时,根据点![]() 的坐标即可得出
的坐标即可得出![]() ;当点
;当点![]() 在线段
在线段![]() 上方时,由抛物线过点
上方时,由抛物线过点![]() 及当
及当![]() 时
时![]() 值大于2,即可得出关于
值大于2,即可得出关于![]() 的一元一次不等式,解之即可得出
的一元一次不等式,解之即可得出![]() .综上即可得出结论.
.综上即可得出结论.
解:![]() 抛物线
抛物线![]() 的顶点
的顶点![]() 位于第一象限且在线段
位于第一象限且在线段![]() 的垂直平分线上,且点
的垂直平分线上,且点![]() ,
,![]() ,
,
![]() ,
,![]() .
.
抛物线与线段![]() 无公共点分两种情况:
无公共点分两种情况:
当点![]() 在线段
在线段![]() 下方时,
下方时,![]() 点
点![]() 的坐标为
的坐标为![]() ,
,
![]() ;
;
当点![]() 在线段
在线段![]() 上方时,有
上方时,有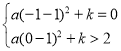 ,
,
解得:![]() .
.
综上所述:![]() 的取值范围为
的取值范围为![]() 或
或![]() .
.
故选:![]() .
.
-
科目: 来源: 题型:
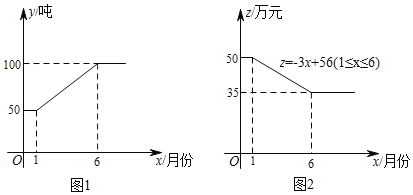
查看答案和解析>>【题目】随着技术的发展进步,某公司2018年采用的新型原料生产产品.这种新型原料的用量y(吨)与月份x之间的关系如图1所示,每吨新型原料所生产的产品的售价z(万元)与月份x之间的关系如图2所示.已知将每吨这种新型原料加工成的产品的成本为20万元.
(1)求出该公司这种新型原料的用量y(吨)与月份x之间的函数关系式;
(2)若该公司利用新型原料所生产的产品当月都全部销售,求哪个月利润最大,最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】点
 是菱形
是菱形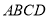 的
的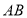 边上一点,点
边上一点,点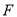 在
在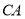 的延长线上
的延长线上(1)如图
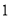 ,若
,若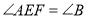 ,
,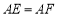 ,求
,求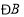 的度数;
的度数;(2)如图
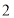 ,若
,若 是
是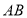 的中点,
的中点,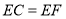 ,求
,求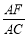 的值;
的值;(3)如图
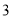 ,若
,若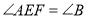 ,点
,点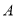 是线段
是线段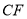 的中点,求证:
的中点,求证: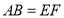

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在
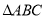 中,
中,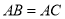 ,求作
,求作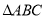 的外心
的外心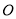 ,以下是甲、乙两同学的作法:对于两人的作法:
,以下是甲、乙两同学的作法:对于两人的作法:甲:如图1,(1)作
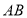 的垂直平分线
的垂直平分线 ;
;(2)作
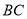 的垂直平分线
的垂直平分线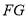 ;
;(3)
 ,
,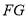 交于点
交于点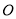 ,则点
,则点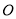 即为所求.
即为所求.乙:如图2,(1)作
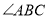 的平分线
的平分线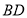 ;
;(2)作
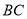 的垂直平分线
的垂直平分线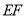 ;
;(3)
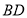 ,
,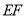 交于点
交于点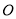 ,则点
,则点 即为所求.
即为所求.
对于两人的作法,正确的是( )
A.两人都对B.两人都不对C.甲对,乙不对D.甲不对,乙对
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为开拓学生视野,开展“课外读书周”活动,活动后期随机调查了九年级部分学生一周的课外阅读时间,并将结果绘制成两幅不完整的统计图,请你根据统计图(图1)的信息回答下列问题:
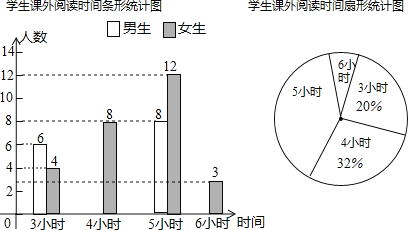
(1)本次调查的学生总数为________人,被调查学生的课外阅读时间的中位数是________小时,众数是_________小时;
(2)请你补全条形统计图,在扇形统计图中,课外阅读时间为
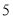 小时的扇形的圆心角度数是_________;
小时的扇形的圆心角度数是_________;(3)若全校九年级共有学生
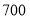 人,估计九年级一周课外阅读时间为
人,估计九年级一周课外阅读时间为 小时的学生有多少人?
小时的学生有多少人?(4)若学校选取
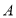 、
、 、
、 、
、 四人参加阅读比赛,两人一组分为两组,求
四人参加阅读比赛,两人一组分为两组,求 与
与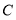 是一组的概率,(列表或树状图)
是一组的概率,(列表或树状图) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点
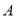 ,
,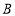 ,
,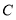 ,
,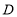 的坐标分别为
的坐标分别为 ,
,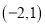 ,
, ,
, .线段
.线段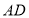 ,
,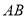 ,
,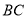 组成的图形为图形
组成的图形为图形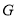 ,点
,点 沿
沿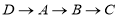 移动,设点
移动,设点 移动的距离为
移动的距离为 ,直线
,直线 过点
过点 ,且在点
,且在点 移动过程中,直线
移动过程中,直线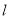 随
随 运动而运动.
运动而运动.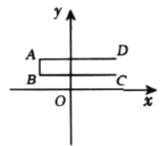
(1)若点
 过点
过点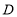 时,求直线
时,求直线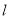 的解析式;
的解析式;(2)当
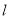 过点
过点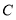 时,求
时,求 值;
值;(3)①若直线
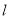 与图形
与图形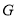 有一个交点,直接写出
有一个交点,直接写出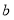 的取值范围;
的取值范围;②若直线
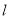 与图形
与图形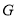 有两个交点,直接写出
有两个交点,直接写出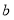 的取值范围.
的取值范围. -
科目: 来源: 题型:
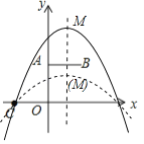
查看答案和解析>>【题目】在高尔夫球训练中,运动员在距球洞
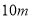 处击球,其飞行路线满足抛物线
处击球,其飞行路线满足抛物线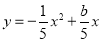 ,其图象如图所示,其中球飞行高度为
,其图象如图所示,其中球飞行高度为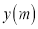 ,球飞行的水平距离为
,球飞行的水平距离为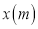 ,球落地时距球洞的水平距离为
,球落地时距球洞的水平距离为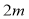 .
.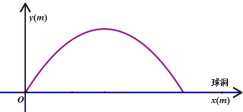
(1)求
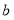 的值;
的值;(2)若运动员再一次从此处击球,要想让球飞行的最大高度不变且球刚好进洞,则球的飞行路线应满足怎样的抛物线,求抛物线的解析式;
(3)若球洞
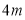 处有一横放的
处有一横放的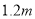 高的球网,球的飞行路线仍满足抛物线
高的球网,球的飞行路线仍满足抛物线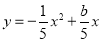 ,要使球越过球网,又不越过球洞(刚好进洞),求
,要使球越过球网,又不越过球洞(刚好进洞),求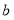 的取值范围.
的取值范围.
相关试题

