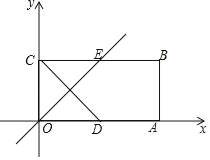
【题目】如图,在平面直角坐标系xOy中,矩形OABC的顶点B的坐标为(4,2),D是OA的中点,OE⊥CD交BC于点E,点P从点O出发,以每秒2个单位长度的速度沿射线OE运动.
(1)求直线OE的解析式;
(2)设以C,P,D,B为顶点的凸四边形的面积为S,点P的运动时间为t(单位:秒),求S关于t的函数解析式,并写出自变量t的取值范围;
(3)设点N为矩形的中心,则在点P运动过程中,是否存在点P,使以P,C,N为顶点的三角形是直角三角形?若存在,请直接写出t的值及点P的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)y=x;(2)S=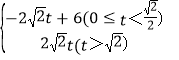 ;(3)存在, t=
;(3)存在, t=![]() 时,P(
时,P(![]() ,
,![]() ),t=
),t=![]() 时,P(2,2),t=
时,P(2,2),t=![]() 时,P(3,3).
时,P(3,3).
【解析】分析: (1)先求出∠COE=45°,进而求出CE=OC=2,即可得出结论;
(2)分点P在OM,在ME,OE的延长线上,利用面积的和差即可得出结论;
(3)分三种情况,利用勾股定理建立方程求出时间t,即可得出结论.
详解:
(1)由题意得,OD=OC=2,
∵OE⊥CD,
∴OE平分∠COD,
∴∠COE=![]() ∠AOC=45°,
∠AOC=45°,
∴OC=CE=2,
∴E(2,2),设直线OE的解析式为y=kx,将点E坐标代入得,2=2k,
∴k=1,
∴直线OE的解析式为y=x;
(2)在Rt△COE中,根据勾股定理得,OE=2![]() ,
,
由题意得,以点C,P,D,B为顶点的图形是四边形,
∴t≠![]() 且t
且t![]() ,
,
分三种情况:
设OE与CD的交点为M,
①当点P在OM上运动时,0≤t<![]() ,
,
S=S矩形OABC﹣S△POC﹣S△POD﹣S△DAB=8﹣![]() ﹣
﹣![]() ﹣2=﹣2
﹣2=﹣2![]() t+6;
t+6;
②当点P在ME上运动时,![]() <t<
<t<![]() ,以点C,P,D,B为顶点的四边形为凹四边形,不符合题意,
,以点C,P,D,B为顶点的四边形为凹四边形,不符合题意,
③点P在OE的延长线上运动时,t>![]() ,
,
S=S△CDB+S△PCB=![]() =2
=2![]() t;
t;
S=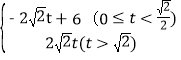 ;
;
(3)存在,理由:PC2=(![]() t)2+(2﹣
t)2+(2﹣![]() t)2=4t2﹣4
t)2=4t2﹣4![]() t+4,PN2=(2﹣
t+4,PN2=(2﹣![]() t)2+(1﹣
t)2+(1﹣![]() t)2=4t2﹣6
t)2=4t2﹣6![]() t+5,NC2=5,
t+5,NC2=5,
①当∠CPN=90°时,PC2+PN2=CN2,
∴4t2﹣4![]() t+4+4t2﹣6
t+4+4t2﹣6![]() t+5=5,
t+5=5,
∴t=![]() 或t=
或t=![]() ;
;
∴P(![]() ,
,![]() )或(2,2);
)或(2,2);
②当∠PNC=90°时,CN2+PN2=PC2,
∴5+4t2﹣6![]() t+5=4t2﹣4
t+5=4t2﹣4![]() t+4,
t+4,
∴t=![]() ,
,
点P(3,3),
③当∠PCN=90°时,PC2+CN2=PN2,4t2﹣4![]() t+4+5=4t2﹣6
t+4+5=4t2﹣6![]() t+5,
t+5,
∴t=﹣![]() ,此时不存在点P,
,此时不存在点P,
即:t=![]() 时,P(
时,P(![]() ,
,![]() ),t=
),t=![]() 时,P(2,2),t=
时,P(2,2),t=![]() 时,P(3,3).
时,P(3,3).
点睛: 此题是一次函数综合题,主要考查了角平分线的性质,待定系数法,几何图形的面积的计算方法,勾股定理,利用勾股定理建立方程是解本题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】近几年,全社会对空气污染问题越来越重视,空气净化器的销量也在逐年增加.某商场从厂家购进了A,B两种型号的空气净化器,两种净化器的销售相关信息见下表:
A型销售数量(台)
B型销售数量(台)
总利润(元)
5
10
2 000
10
5
2 500
(1)每台A型空气净化器和B型空气净化器的销售利润分别是多少?
(2)该公司计划一次购进两种型号的空气净化器共100台,其中B型空气净化器的进货量不少于A型空气净化器的2倍,为使该公司销售完这100台空气净化器后的总利润最大,请你设计相应的进货方案;
(3)已知A型空气净化器的净化能力为300 m3/小时,B型空气净化器的净化能力为200 m3/小时.某长方体室内活动场地的总面积为200 m2,室内墙高3 m.该场地负责人计划购买5台空气净化器每天花费30分钟将室内空气净化一新,如不考虑空气对流等因素,至少要购买A型空气净化器多少台?
-
科目: 来源: 题型:
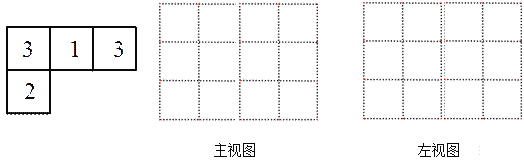
查看答案和解析>>【题目】由一些大小相同,棱长为1的小正方体搭成的几何体的俯视图如图所示,数字表示该位置的正方体个数.
(1)请画出它的主视图和左视图;
(2)给这个几何体喷上颜色(底面不喷色),需要喷色的面积为
(3)在不改变主视图和俯视图的情况下,最多可添加 块小正方体.
-
科目: 来源: 题型:
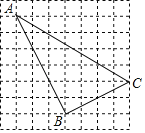
查看答案和解析>>【题目】已知图中的每个方格都是边长为1的小正方形,每个小正方形的顶点称为格点,△ABC的顶点在格点上,称为格点三角形,请按要求完成下列各题
(1)填空:
AB= ,BC= ,AC= ;
(2)试判断△ABC的形状,并说明理由.
-
科目: 来源: 题型:
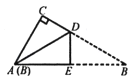
查看答案和解析>>【题目】如图,有一直角三角形纸片ABC,∠C=90°,∠B=30°,将该直角三角形纸片沿DE折叠,使点B与点A重合,DE=1,则BC的长度为( )
A. 2 B.
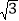 +2 C. 3 D. 2
+2 C. 3 D. 2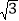
-
科目: 来源: 题型:
查看答案和解析>>【题目】小梅在浏览某电影评价网站时,搜索了最近关注到的甲、乙、丙三部电影,网站通过对观众的抽样调查,得到这三部电影的评分数据统计图分别如下:
甲、乙、丙三部电影评分情况统计图
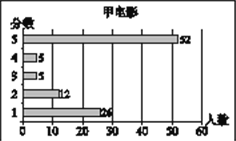


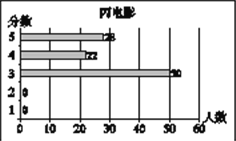
根据以上材料回答下列问题:
(1)小梅根据所学的统计知识,对以上统计图中的数据进行了分析,并通过计算得到这三部电影抽样调查的样本容量,观众评分的平均数、众数、中位数,请你将下表补充完整:
甲、乙、丙三部电影评分情况统计表
电影
样本容量
平均数
众数
中位数
甲
100
3.45
5
乙
3.66
5
丙
100
3
3.5
(2)根据统计图和统计表中的数据,可以推断其中_______电影相对比较受欢迎,理由是
_______________________________________________________________________.(至少从两个不同的角度说明你推断的合理性)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某水果批发市场规定,一次购买苹果不超过100kg(包括100kg),批发价为5元,如果一次购买100kg以上苹果,超过100kg的部分苹果价格打8折.
(I)请填写下表
购买量/kg
0
50
100
150
200
…
付款金额/元
0
250
_
700
__
…
(Ⅱ)写出付款金额关于购买量的函数解析式;
(Ⅲ)如果某人付款2100元,求其购买苹果的数量.
相关试题

