【题目】如图,△ABC中,∠BAC=60°,
(1)如果△ABC角平分线BD、CE相交与点O,则∠BOC_________。
(2)如果△ABC的高BD、CE相交与点O,求∠BOC的度数。


参考答案:
【答案】(1)=120;(2)∠BOC =120°.
【解析】
(1)根据三角形内角和定理和角平分线定义求出∠OBC+∠OCB的度数,然后在△BOC中通过三角形内角和定理可求出∠BOC的度数;
(2)由高线的定义可知∠AEC=90°,∠ADB=90°,然后根据四边形内角和定理可求出∠DOE,问题得解.
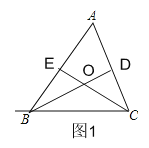
解(1)如图1,
∵∠BAC=60°,
∴∠ABC+∠ACB=180°-∠BAC=120°,
∵BD、CE分别是∠ABC,∠ACB的角平分线,
∴∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,
∠ACB,
∴∠OBC+∠OCB=![]() ∠ABC+
∠ABC+![]() ∠ACB=
∠ACB=![]() (∠ACB+∠ACB)=60°,
(∠ACB+∠ACB)=60°,
∴∠BOC=180°-(∠OBC+∠OCB)=120°;
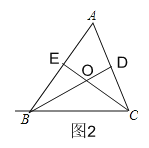
(2)如图2,
∵∠BAC=60°,BD、CE是△ABC的高线,
∴∠AEC=90°,∠ADB=90°,
∴∠DOE=360°-∠BAC-∠AEC-∠ADB=360°-60°-90°-90°=120°,
∴∠BOC=∠DOE=120°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次数学兴趣小组活动中,同学们做了一个找朋友的游戏:有六个同学A、B、C、D、E、F分别藏在六张大纸牌的后面,如图,A、B、C、D、E、F所持的纸牌的前面分别写有六个算式:66;63+63;(63)3;(2×62)×(3×63);(22×32)3;(64)3÷62.游戏规定:所持算式的值相等的两个人是朋友.如果现在由同学A来找他的朋友,他可以找谁呢?说说你的看法.
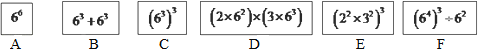
-
科目: 来源: 题型:
查看答案和解析>>【题目】为宣传6月6日世界海洋日,某校八年级举行了主题为“珍惜海洋资源,保护海洋生物多样性”的知识竞赛活动.为了解全年级500名学生此次竞赛成绩(百分制)的情况,随机抽取了部分参赛学生的成绩,整理并绘制出如下不完整的统计表(表1)和统计图(如图).请根据图表信息解答以下问题:

(1)本次调查一共随机抽取了个参赛学生的成绩;
(2)表1中a= ;
(3)所抽取的参赛学生的成绩的中位数落在的“组别”是 ;
(4)请你估计,该校九年级竞赛成绩达到90分以上(含90分)的学生约有多少人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB>AC,点D、E分别是边AB、AC的中点,点F在BC边上,连接DE、DF、EF,则添加下列哪一个条件后,仍无法判断△FCE与△EDF全等( )
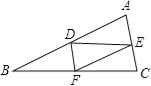
A. ∠A=∠DFE B. BF=CF C. DF∥AC D. ∠C=∠EDF
-
科目: 来源: 题型:
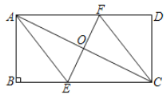
查看答案和解析>>【题目】如图,在矩形
 中,点
中,点 为对角线
为对角线 的中点,过点
的中点,过点 作
作 交
交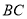 于点
于点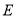 ,交
,交 于点
于点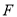 ,连接
,连接 ,
,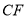 .
.
(1)求证:四边形
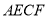 是菱形;
是菱形;(2)连接
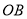 ,若
,若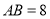 ,
,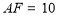 ,求
,求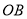 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠MON=ɑ(0°<ɑ<180°),点A.B分别在OM、ON上运动(不与点O重合).
(1)如图1,∠MON=90°,BC是∠ABN的平分线,BC的反方向延长线与∠BAO的平分线交与点D.
①若∠BAO=60°,则∠D=___.
②猜想:∠D的度数是否随A,B的移动发生变化?并说明理由。
(2)如图2,∠MON=α(0°<α<180°)”,∠ABC=
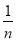 ∠ABN,∠BAD=
∠ABN,∠BAD=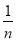 ∠BAO,其余条件不变,则∠D=___°(用含α、n的代数式表示)
∠BAO,其余条件不变,则∠D=___°(用含α、n的代数式表示)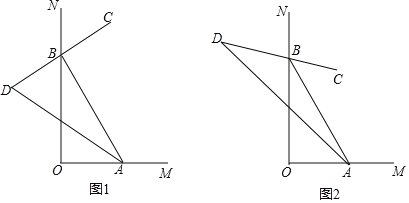
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图矩形ABCD中,AB=3cm,AD=9cm,将此矩形折叠,使点B与点D重合,折痕为EF.
(1)求证:BE=BF;
(2)求△ABE的面积;
(3)求折痕EF的长.

相关试题

