【题目】如图,在矩形![]() 中,点
中,点![]() 为对角线
为对角线![]() 的中点,过点
的中点,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
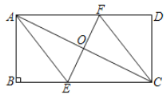
(1)求证:四边形![]() 是菱形;
是菱形;
(2)连接![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
参考答案:
【答案】(1)见解析 (2)![]()
【解析】
(1)由矩形的性质可得∠ACB=∠DAC,然后利用“ASA”证明△AOF和△COE全等,根据全等三角形对应边相等可得OE=OF,即可证四边形AECF是菱形;
(2)连接BD,![]() ,根据平行四边形的性质可得AF=CF=10,用勾股定理求得FD=6,在△BDC中,∠DCB=90°,用勾股定理求出BD的值,即可解答.
,根据平行四边形的性质可得AF=CF=10,用勾股定理求得FD=6,在△BDC中,∠DCB=90°,用勾股定理求出BD的值,即可解答.
(1)∵四边形ABCD是矩形,
∴AD∥BC,
∴∠ACB=∠DAC,
∵O是AC的中点,
∴AO=CO,
在△AOF和△COE中,

∴△AOF≌△COE(ASA),
∴OE=OF,且AO=CO,
∴四边形AECF是平行四边形,
又∵EF⊥AC,
∴四边形AECF是菱形;
(2)连接BD,![]()

![]() 四边形AFCE是平行四边形
四边形AFCE是平行四边形
![]() AF=CF=10
AF=CF=10
![]() ∠CDF=90°
∠CDF=90°
![]()
![]() CF=10,CD=AB=8
CF=10,CD=AB=8
![]() FD=6
FD=6
![]() AD=AF+DF=6+10=16
AD=AF+DF=6+10=16
![]() ∠DAB=90°
∠DAB=90°
![]() =
=![]() =
=![]()
![]() BO=
BO=![]()
故答案为:![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】为宣传6月6日世界海洋日,某校八年级举行了主题为“珍惜海洋资源,保护海洋生物多样性”的知识竞赛活动.为了解全年级500名学生此次竞赛成绩(百分制)的情况,随机抽取了部分参赛学生的成绩,整理并绘制出如下不完整的统计表(表1)和统计图(如图).请根据图表信息解答以下问题:

(1)本次调查一共随机抽取了个参赛学生的成绩;
(2)表1中a= ;
(3)所抽取的参赛学生的成绩的中位数落在的“组别”是 ;
(4)请你估计,该校九年级竞赛成绩达到90分以上(含90分)的学生约有多少人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB>AC,点D、E分别是边AB、AC的中点,点F在BC边上,连接DE、DF、EF,则添加下列哪一个条件后,仍无法判断△FCE与△EDF全等( )
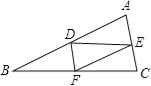
A. ∠A=∠DFE B. BF=CF C. DF∥AC D. ∠C=∠EDF
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠BAC=60°,
(1)如果△ABC角平分线BD、CE相交与点O,则∠BOC_________。
(2)如果△ABC的高BD、CE相交与点O,求∠BOC的度数。


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠MON=ɑ(0°<ɑ<180°),点A.B分别在OM、ON上运动(不与点O重合).
(1)如图1,∠MON=90°,BC是∠ABN的平分线,BC的反方向延长线与∠BAO的平分线交与点D.
①若∠BAO=60°,则∠D=___.
②猜想:∠D的度数是否随A,B的移动发生变化?并说明理由。
(2)如图2,∠MON=α(0°<α<180°)”,∠ABC=
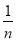 ∠ABN,∠BAD=
∠ABN,∠BAD=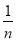 ∠BAO,其余条件不变,则∠D=___°(用含α、n的代数式表示)
∠BAO,其余条件不变,则∠D=___°(用含α、n的代数式表示)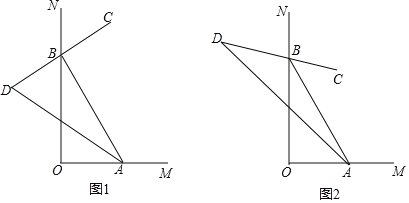
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图矩形ABCD中,AB=3cm,AD=9cm,将此矩形折叠,使点B与点D重合,折痕为EF.
(1)求证:BE=BF;
(2)求△ABE的面积;
(3)求折痕EF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某电器商场销售A、B两种型号计算器,两种计算器的进货价格分别为每台30元,40元,商场销售5台A型号和1台B型号计算器,可获利润76元;销售6台A型号和3台B型号计算器,可获利润120元.求商场销售A、B两种型号计算器的销售价格分别是多少元?(利润=销售价格﹣进货价格)
相关试题

