搜索
【题目】从①
；②
；③
；④
．这四个条件中选取两个，使四边形
成为平行四边形．下面不能说明是平行四边形的是（ ）
A.①②B.①③C.②④D.①④
参考答案：
【答案】D
【解析】
根据平行四边形的判定方法逐项判断即可．
解：A、选①②，即四边形ABCD满足
，
，根据一组对边平行且相等的四边形是平行四边形可判定四边形ABCD是平行四边形，故本选项不符合题意；
B、选①③，即四边形ABCD满足，
，根据两组对边分别平行的四边形是平行四边形可判定四边形ABCD是平行四边形，故本选项不符合题意；
C、选②④，即四边形ABCD满足，
，根据两组对边分别相等的四边形是平行四边形可判定四边形ABCD是平行四边形，故本选项不符合题意；
D、选①④，即四边形ABCD满足，，一组对边平行，另一组对边相等，不能判定四边形ABCD是平行四边形，故本选项符合题意．
故选：D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在同一个直角坐标系中作出y＝
x2，y＝x2－1的图象．(1)分别指出它们的开口方向、对称轴以及顶点坐标；
(2)抛物线y＝
x2－1与抛物线y＝x2有什么关系？ -
科目： 来源： 题型：
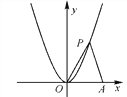
查看答案和解析>>【题目】如图，点P是抛物线y＝x2在第一象限内的一点，点A的坐标是(3，0)．设点P的坐标为(x，y)．
(1)求△OPA的面积S关于变量y的关系式；
(2)S是x的什么函数？
(3)当S＝6时，求点P的坐标；
(4)在y＝x2的图象上求一点P′，使△OP′A的两边OP′＝P′A.
-
科目： 来源： 题型：
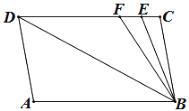
查看答案和解析>>【题目】如图，已知直线AB∥CD，∠A=∠C=100°，E、F在CD上，且满足∠DBF=∠ABD，BE平分∠CBF．
（1）直线AD与BC有何位置关系？请说明理由.
（2）求∠DBE的度数．
（3）若把AD左右平行移动，在平行移动AD的过程中，是否存在某种情况，使∠BEC=∠ADB？若存在，求出此时∠ADB的度数；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】当行驶中的汽车撞到物体时，汽车的损坏程度通常用“撞击影响”来衡量．汽车的撞击影响I可以用汽车行驶速度v(km/min)来表示，下表是某种型号汽车的行驶速度与撞击影响的试验数据：
v(km/min)
0
1
2
3
4
I
0
2
8
18
32
(1)请根据上表中的数据，在直角坐标系中描出坐标(v，I)所对应的点，并用光滑曲线将各点连接起来；
(2)填写下表，并根据表中数据的呈现规律，猜想用v表示I的二次函数表达式；
v(km/min)
1
2
3
4
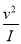
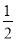
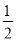
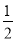
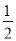
(3)当汽车的速度分别是1.5 km/min，2.5 km/min，4.5 km/min时，利用你得到的撞击影响公式，计算撞击影响分别是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】某学校为了解学生的课外阅读情况，随机抽取了50名学生，并统计他们平均每天的课外阅读时间t（单位：min），然后利用所得数据绘制成如下不完整的统计表．
课外阅读时间t
频数
百分比
10≤t＜30
4
8%
30≤t＜50
8
16%
50≤t＜70
a
40%
70≤t＜90
16
b
90≤t＜110
2
4%
合计
50
100%
请根据图表中提供的信息回答下列问题：
（1）a= ，b= ；
（2）将频数分布直方图补充完整；
（3）若全校有900名学生，估计该校有多少学生平均每天的课外阅读时间不少于50min？
-
科目： 来源： 题型：
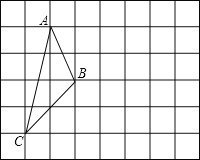
查看答案和解析>>【题目】如图，在方格纸中，每个小正方形的边长均为1个单位长度有一个△ABC，它的三个顶点均与小正方形的顶点重合．
（1）将△ABC向右平移3个单位长度，得到△DEF（A与D、B与E、C与F对应），请在方格纸中画出△DEF；
（2）在（1）的条件下，连接AE和CE，请直接写出△ACE的面积S，并判断B是否在边AE上．
相关试题
