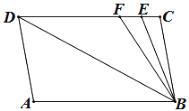
【题目】如图,已知直线AB∥CD,∠A=∠C=100°,E、F在CD上,且满足∠DBF=∠ABD,BE平分∠CBF.
(1)直线AD与BC有何位置关系?请说明理由.
(2)求∠DBE的度数.
(3)若把AD左右平行移动,在平行移动AD的过程中,是否存在某种情况,使∠BEC=∠ADB?若存在,求出此时∠ADB的度数;若不存在,请说明理由.
参考答案:
【答案】(1) AD∥BC,理由见解析;(2) 40°;(3)存在,∠ADB=60°
【解析】试题分析:(1)根据平行线的性质,以及等量代换证明∠ADC+∠C=180°,即可证得AD∥BC;(2)由直线AB∥CD,根据两直线平行,同旁内角互补,即可求得∠ABC的度数,又由∠DBE=![]() ∠ABC,即可求得∠DBE的度数.
∠ABC,即可求得∠DBE的度数.
(3)首先设∠ABD=∠DBF=∠BDC=x°,由直线AB∥CD,根据两直线平行,同旁内角互补与两直线平行,内错角相等,可求得∠BEC与∠ADB的度数,又由∠BEC=∠ADB,即可得方程:x°+40°=80°-x°,解此方程即可求得答案.
试题解析:(1)AD∥BC
理由:∵AB∥CD,
∴∠A+∠ADC=180°,
又∵∠A=∠C
∴∠ADC+∠C=180°,
∴AD∥BC;
(2)∵AB∥CD,
∴∠ABC=180°-∠C=80°,
∵∠DBF=∠ABD,BE平分∠CBF,
∴∠DBE=![]() ∠ABF+
∠ABF+![]() ∠CBF=
∠CBF=![]() ∠ABC=40°;
∠ABC=40°;
(3)存在.
理由:设∠ABD=∠DBF=∠BDC=x°.
∵AB∥CD,
∴∠BEC=∠ABE=x°+40°;
∵AB∥CD,
∴∠ADC=180°-∠A=80°,
∴∠ADB=80°-x°.
若∠BEC=∠ADB,
则x°+40°=80°-x°,
得x°=20°.
∴存在∠BEC=∠ADB=60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把y=
 x2的图象向上平移2个单位.
x2的图象向上平移2个单位.(1)求新图象的解析式、顶点坐标和对称轴;
(2)画出平移后的函数图象;
(3)求平移后的函数的最大值或最小值,并求对应的x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一个直角坐标系中作出y=
 x2,y=
x2,y= x2-1的图象.
x2-1的图象.(1)分别指出它们的开口方向、对称轴以及顶点坐标;
(2)抛物线y=
 x2-1与抛物线y=
x2-1与抛物线y= x2有什么关系?
x2有什么关系? -
科目: 来源: 题型:
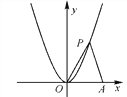
查看答案和解析>>【题目】如图,点P是抛物线y=x2在第一象限内的一点,点A的坐标是(3,0).设点P的坐标为(x,y).
(1)求△OPA的面积S关于变量y的关系式;
(2)S是x的什么函数?
(3)当S=6时,求点P的坐标;
(4)在y=x2的图象上求一点P′,使△OP′A的两边OP′=P′A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从①
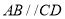 ;②
;②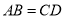 ;③
;③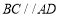 ;④
;④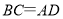 .这四个条件中选取两个,使四边形
.这四个条件中选取两个,使四边形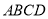 成为平行四边形.下面不能说明是平行四边形的是( )
成为平行四边形.下面不能说明是平行四边形的是( )A.①②B.①③C.②④D.①④
-
科目: 来源: 题型:
查看答案和解析>>【题目】当行驶中的汽车撞到物体时,汽车的损坏程度通常用“撞击影响”来衡量.汽车的撞击影响I可以用汽车行驶速度v(km/min)来表示,下表是某种型号汽车的行驶速度与撞击影响的试验数据:
v(km/min)
0
1
2
3
4
I
0
2
8
18
32
(1)请根据上表中的数据,在直角坐标系中描出坐标(v,I)所对应的点,并用光滑曲线将各点连接起来;

(2)填写下表,并根据表中数据的呈现规律,猜想用v表示I的二次函数表达式;
v(km/min)
1
2
3
4
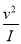
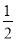
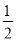
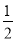
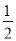
(3)当汽车的速度分别是1.5 km/min,2.5 km/min,4.5 km/min时,利用你得到的撞击影响公式,计算撞击影响分别是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了解学生的课外阅读情况,随机抽取了50名学生,并统计他们平均每天的课外阅读时间t(单位:min),然后利用所得数据绘制成如下不完整的统计表.
课外阅读时间t
频数
百分比
10≤t<30
4
8%
30≤t<50
8
16%
50≤t<70
a
40%
70≤t<90
16
b
90≤t<110
2
4%
合计
50
100%
请根据图表中提供的信息回答下列问题:
(1)a= ,b= ;
(2)将频数分布直方图补充完整;
(3)若全校有900名学生,估计该校有多少学生平均每天的课外阅读时间不少于50min?

相关试题

