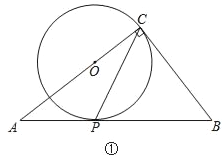
【题目】在△ABC中,∠ACB=90°,经过点C的⊙O与斜边AB相切于点P.
(1)如图①,当点O在AC上时,试说明2∠ACP=∠B;
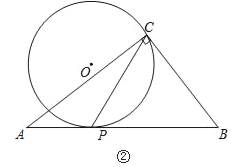
(2)如图②,AC=8,BC=6,当点O在△ABC外部时,求CP长的取值范围.
参考答案:
【答案】(1)2∠ACP=∠B;(2)当点O在△ABC外时,![]() <CP≤8.
<CP≤8.
【解析】分析:(1)根据BC与AC垂直得到BC与圆相切,再由AB与![]() 相切于点P,利用切线长定理得到
相切于点P,利用切线长定理得到![]() ,利用等边对等角得到一对角相等,再由
,利用等边对等角得到一对角相等,再由![]() 等量代换即可得证;
等量代换即可得证;
(2)在![]() 中,利用勾股定理求出AB的长,根据AC与BC垂直,得到BC与
中,利用勾股定理求出AB的长,根据AC与BC垂直,得到BC与![]() 相切,连接连接OP、AO,再由AB与
相切,连接连接OP、AO,再由AB与![]() 相切,得到OP垂直于AB,设OC=x,则OP=x,OB=BCOC=6x,求出PA的长,利用勾股定理列出关于x的方程,求出方程的解得到x的值,确定出BO的长,根据AC=AP,OC=OP,得到AO垂直平分CP,根据面积法求出CP的长,由题意可知,当点P与点A重合时,CP最长,即可确定出CP的范围.
相切,得到OP垂直于AB,设OC=x,则OP=x,OB=BCOC=6x,求出PA的长,利用勾股定理列出关于x的方程,求出方程的解得到x的值,确定出BO的长,根据AC=AP,OC=OP,得到AO垂直平分CP,根据面积法求出CP的长,由题意可知,当点P与点A重合时,CP最长,即可确定出CP的范围.
详解:(1)当点O在AC上时,OC为![]() 的半径,
的半径,
∵BC⊥OC,且点C在![]() 上,
上,
∴BC与![]() 相切,
相切,
∵![]() 与AB边相切于点P,
与AB边相切于点P,
∴BC=BP,
∴![]()
∵![]()
∴![]()
即2∠ACP=∠B;
(2)在△ABC中, ![]()
如图,当点O在CB上时,OC为![]() 的半径,
的半径,
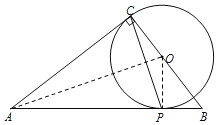
∵AC⊥OC,且点C在![]() 上,
上,
∴AC与![]() 相切,
相切,
连接OP、AO,
∵![]() 与AB边相切于点P,
与AB边相切于点P,
∴OP⊥AB,
设OC=x,则OP=x,OB=BCOC=6x,
∵AC=AP,
∴BP=ABAP=108=2,
在△OPA中,![]()
根据勾股定理得:![]() ,即
,即![]()
解得:![]()
在△ACO中,![]()
∴![]()
∵AC=AP,OC=OP,
∴AO垂直平分CP,
∴根据面积法得:![]() 则符合条件的CP长大于
则符合条件的CP长大于![]()
由题意可知,当点P与点A重合时,CP最长,
综上,当点O在△ABC外时,![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两根高度分别是
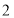 米和
米和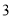 米的直杆
米的直杆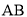 、
、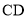 竖直在水平地面
竖直在水平地面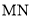 上,相距
上,相距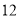 米,现要从
米,现要从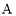 点拉一根绳索,接地后再拉到
点拉一根绳索,接地后再拉到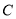 点处,为了节省绳索材料,请问:
点处,为了节省绳索材料,请问:
(1)根据你学过的知识,在地面上确定绳索接地的位置(用点
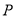 表示),使绳索的长度最短.
表示),使绳索的长度最短. (2)求绳索的最短长度(不计接头部分).
-
科目: 来源: 题型:
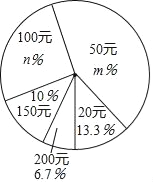
查看答案和解析>>【题目】某中学在一次爱心捐款活动中,全体同学积极踊跃捐款.现抽查了九年级(1)班全班同学捐款情况,并绘制出如下的统计表和统计图:
捐款(元)
20
50
100
150
200
人数(人)
4
12
9
3
2
求:(Ⅰ)m=_____,n=_____;
(Ⅱ)求学生捐款数目的众数、中位数和平均数;
(Ⅲ)若该校有学生2500人,估计该校学生共捐款多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在中
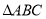 ,
,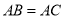 ,
,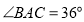 ,
,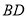 是
是 的平分线,交
的平分线,交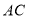 于点
于点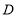 ,
,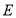 是
是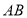 的中点,连接
的中点,连接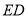 并延长交
并延长交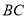 的延长线于点
的延长线于点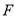 ,连接
,连接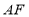 .
.求证:(1)
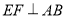 ;
;(2)
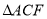 为等腰三角形
为等腰三角形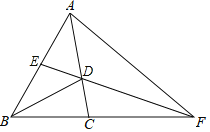
-
科目: 来源: 题型:
查看答案和解析>>【题目】在甲村至乙村间有一条公路,在C处需要爆破,已知点C与公路上的停靠站A的距离为300米,与公路上的另一停靠站B的距离为400米,且CA⊥CB,如图所示.为了安全起见,爆破点C周围半径250米范围内不得进入,问在进行爆破时,公路AB段是否有危险?请用你学过的知识加以解答.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠BAC=90°,AC=AB,点D为直线BC上的一动点,以AD为边作△ADE(顶点A、D、E按逆时针方向排列),且∠DAE=90°,AD=AE,连接CE.
⑴ 如图1,若点D在BC边上(点D与B、C不重合),求∠BCE的度数.
⑵ 如图2,若点D在CB的延长线上,若DB=5,BC=7,求△ADE的面积.

-
科目: 来源: 题型:
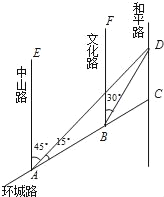
查看答案和解析>>【题目】如图,AC是某市环城路的一段,AE,BF,CD都是南北方向的街道,其与环城路AC的交叉路口分别是A,B,C.经测量花卉世界D位于点A的北偏东45°方向,点B的北偏东30°方向上,AB=2km,∠DAC=15°.
(1)求B,D之间的距离;
(2)求C,D之间的距离.
相关试题

