【题目】如图1,过等边三角形ABC边AB上一点D作DE∥BC交边AC于点E,分别取BC,DE的中点M,N,连接MN.
(1)发现:在图1中, ![]() =;
=;
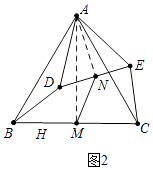
(2)应用:如图2,将△ADE绕点A旋转,请求出 ![]() 的值;
的值;
(3)拓展:如图3,△ABC和△ADE是等腰三角形,且∠BAC=∠DAE,M,N分别是底边BC,DE的中点,若BD⊥CE,请直接写出 ![]() 的值.
的值.
参考答案:
【答案】
(1)![]()
(2)
解:如图2中,连接AM、AN.
∵△ABC,△ADE都是等边三角形,BM=MC,DN=NE,
∴AM⊥BC,AN⊥DE,
∴ ![]() =sin60°,
=sin60°, ![]() =sin60°,
=sin60°,
∴ ![]() =
= ![]() ,
,
∵∠MAB=∠DAN=30°,
∴∠BAD=∠MAN,
∴△BAD∽△MAN,
∴ ![]() =
= ![]() =sin60°=
=sin60°= ![]()
(3)
解:如图3中,连接AM、AN,延长AD交CE于H,交AC于O.
∵AB=AC,AD=AE,BM=CM,DN=NE,
∴AM⊥BC,AN⊥DE,
∵∠BAC=∠DAE,
∴∠ABC=∠ADE,
∴sin∠ABM=sin∠ADN,
∴ ![]() =
= ![]() ,
,
∵∠BAM= ![]() BAC,∠DAN=
BAC,∠DAN= ![]() ∠DAE,
∠DAE,
∴∠BAM=∠DAN,
∴∠BAD=∠MAN.
∴△BAD∽△MAN,
∴ ![]() =
= ![]() =sin∠ABC,
=sin∠ABC,
∵∠BAC=∠DAE,
∴∠BAD=∠CAE,
∵AB=AC,AD=AE,
∴△BAD≌△CAE,
∴∠ABD=∠ACE,
∵BD⊥CE,
∴∠BHC=90°,
∴∠ACE+∠COH=90°,∵∠AOB=∠COH,
∴∠ABD+∠AOB=90°,
∴∠BAO=90°,
∵AB=AC,
∴∠ABC=45°,
∴ ![]() =sin45°=
=sin45°= ![]()

【解析】解:(1)如图1中,作DH⊥BC于H,连接AM.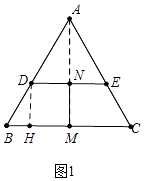
∵AB=AC,BM=CM,
∴AM⊥BC,
∵△ADE时等边三角形,
∴∠ADE=60°=∠B,
∴DE∥BC,
∵AM⊥BC,
∴AM⊥DE,
∴AM平分线段DE,
∵DN=NE,
∴A、N、M共线,
∴∠NMH=∠MND=∠DHM=90°,
∴四边形MNDH时矩形,
∴MN=DH,
∴ ![]() =
= ![]() =sin60°=
=sin60°= ![]() ,
,
所以答案是 ![]() .
.
【考点精析】解答此题的关键在于理解相似三角形的性质的相关知识,掌握对应角相等,对应边成比例的两个三角形叫做相似三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】按图中方式用火柴棒搭正方形

①搭1个正方形需要 根火柴棒;
②搭2个正方形需要 根火柴棒,搭3个正方形需要 根火柴棒;
③搭10个这样的正方形需要多少根火柴棒;
④搭100个这样的正方形需要多少根火柴棒?
⑤如果用x表示所搭正方形的个数,那么搭x个这样的正方形需要多少根火柴棒?与同伴交流。
⑥根据你的计算方法,搭200个这样的正方形需要多少根火柴棒?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段AB=8cm,C是线段AB上一点,AC=3.2cm,M是AB的中点,N是AC的中点.
(1)求线段CM的长;
(2)求线段MN的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,直线y=﹣x+1与抛物线y=ax2+bx+c(a≠0)相交于点A(1,0)和点D(﹣4,5),并与y轴交于点C,抛物线的对称轴为直线x=﹣1,且抛物线与x轴交于另一点B.

(1)求该抛物线的函数表达式;
(2)若点E是直线下方抛物线上的一个动点,求出△ACE面积的最大值;
(3)如图2,若点M是直线x=﹣1的一点,点N在抛物线上,以点A,D,M,N为顶点的四边形能否成为平行四边形?若能,请直接写出点M的坐标;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一条不完整的数轴上从左到右有点A,B,C,其中AB=2,BC=1,如图所示.设点A,B,C所对应数的和是p.

(1)若以B为原点,写出点A,C所对应的数,并计算p的值;若以C为原点,p又是多少?
(2)若原点O在图中数轴上点C的右边,且CO=28,求p.
-
科目: 来源: 题型:
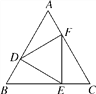
查看答案和解析>>【题目】如图,△ABC是等边三角形,点D,E,F分别是AB,BC,CA上的点.
(1)若AD=BE=CF,问△DEF是等边三角形吗?试证明你的结论;
(2)若△DEF是等边三角形,问AD=BE=CF成立吗?试证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(0,2),△AOB为等边三角形,P是x轴上一个动点(不与原O重合),以线段AP为一边在其右侧作等边三角形△APQ.

(1)求点B的坐标;
(2)在点P的运动过程中,∠ABQ的大小是否发生改变?如不改变,求出其大小;如改变,请说明理由.
(3)连接OQ,当OQ∥AB时,求P点的坐标.
相关试题

