【题目】问题探究
(1)如图1,请在半径为![]() 的半圆
的半圆![]() 内(含弧和直径
内(含弧和直径![]() )画出面积最大的三角形,并求出这个三角形的面积;
)画出面积最大的三角形,并求出这个三角形的面积;
(2)如图2,请在半径为![]() 的
的![]() 内(含弧)画出面积最大的矩形
内(含弧)画出面积最大的矩形![]() ,并求出这个矩形的面积;
,并求出这个矩形的面积;
问题解决
(3)如图3,![]() 是一块草坪,其中
是一块草坪,其中![]() ,
,![]() ,
,![]() ,某开发商现准备再征一块地,把
,某开发商现准备再征一块地,把![]() 扩充为四边形
扩充为四边形![]() ,使
,使![]() ,是否存在面积最大的四边形
,是否存在面积最大的四边形![]() ?若存在,求出四边形
?若存在,求出四边形![]() 的最大面积;若不存在,请说明理由.(结果保留根号)
的最大面积;若不存在,请说明理由.(结果保留根号)
参考答案:
【答案】(1)图形见解析;![]() ;(2)图形见解析;
;(2)图形见解析;![]() 矩形
矩形![]() ;(3)存在,最大面积为
;(3)存在,最大面积为![]() .
.
【解析】
(1)过圆心O作直径的垂线得到最大的![]() ,求面积即可;
,求面积即可;
(2)作两条互相垂直的直径,作对角线,连成的四边形即为最大的矩形,求其面积即可;
(3)如图3,过A作AE⊥BC,交CB的延长线于E,分别求出EC、AE、AC的长,求![]() 的面积,在
的面积,在![]() 中,AC是定值,∠D=30°是定值,画
中,AC是定值,∠D=30°是定值,画![]() 的外接圆O,由图3可知:当D点与AC的距离最大时,
的外接圆O,由图3可知:当D点与AC的距离最大时,![]() 的面积最大,设AC的中垂线交⊙O于
的面积最大,设AC的中垂线交⊙O于![]() ,交AC于F,则
,交AC于F,则![]() 即为D点与AC的最大距离,求出
即为D点与AC的最大距离,求出![]() ,代入面积公式求面积即可.
,代入面积公式求面积即可.
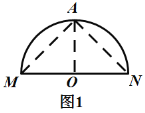
解:(1)如图1,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,则
,则![]() 即为所求.
即为所求.
![]()
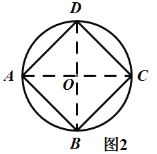
(2)如图2,过点![]() 作
作![]() 的任一直径
的任一直径![]() ,再过点
,再过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() 、
、![]() ,连接
,连接![]() 、
、![]() 、
、![]() 、
、![]() ,则矩形
,则矩形![]() 即为所求.
即为所求.
![]() 矩形
矩形![]() ;
;
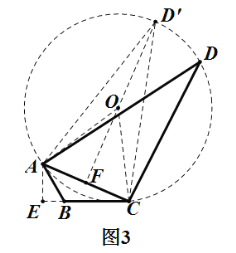
(3)存在面积最大的四边形![]() ,理由如下:
,理由如下:
如图3,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
![]() .
.
![]() ,
,
![]() .
.
在![]() 中,
中,![]() 是定值,
是定值,![]() 是定值,
是定值,
如图3,![]() 、
、![]() 、
、![]() 三点在同一
三点在同一![]() 上(作
上(作![]() 、
、![]() 的中垂线,交点即为圆心
的中垂线,交点即为圆心![]() ),
),
![]() 的长度一定,
的长度一定,
![]() 当
当![]() 点与
点与![]() 的距离最大时,
的距离最大时,![]() 的面积最大.
的面积最大.
设![]() 的中垂线交
的中垂线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,
则![]() 即为
即为![]() 点与
点与![]() 的最大距离.
的最大距离.
![]() ,
,
连接![]() 、
、![]() ,则
,则![]() 。
。
![]() 是等边三角形.
是等边三角形.
![]() ,
,![]() .
.
∴![]() .
.
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]()
即四边形![]() 的最大面积为
的最大面积为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四张编号为A,B,C,D的卡片(除编号外,其余完全相同)的正面分别写上如图所示的正整数后,背面向上,洗匀放好.

(1)我们知道,满足a2+b2=c2的三个正整数a,b,c成为勾股数,嘉嘉从中随机抽取一张,求抽到的卡片上的数是勾股数的概率P1;
(2)琪琪从中随机抽取一张(不放回),再从剩下的卡片中随机抽取一张(卡片用A,B,C,D表示).请用列表或画树形图的方法求抽到的两张卡片上的数都是勾股数的概率P2 , 并指出她与嘉嘉抽到勾股数的可能性一样吗? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,点E、F、H分别是AB、BC、CD的中点,CE、DF交于G,连接AG、HG.下列结论:①CE⊥DF;②AG=AD;③∠CHG=∠DAG;④HG=
 AD.其中正确的有( )
AD.其中正确的有( )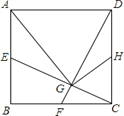
A. ① ② B. ① ② ④ C. ① ③ ④ D. ① ② ③ ④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
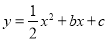 与
与 轴交于
轴交于 和
和 两点,与
两点,与 轴交于
轴交于 点.
点.(1)求此抛物线的解析式;
(2)设
 是线段
是线段 上的动点,作
上的动点,作 交
交 于
于 ,连接
,连接 ,当
,当 的面积是
的面积是 面积的2倍时,求
面积的2倍时,求 点的坐标;
点的坐标;(3)若
 为抛物线上
为抛物线上 、
、 两点间的一个动点,过
两点间的一个动点,过 作
作 轴的平行线,交
轴的平行线,交 于
于 ,当
,当 点运动到什么位置时,线段
点运动到什么位置时,线段 的值最大,并求此时
的值最大,并求此时 点的坐标.
点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,斜坡AP的坡度为1:2.4,坡长AP为26米,在坡顶A处的同一水平面上有一座古塔BC,在斜坡底P处测得该塔的塔顶B的仰角为45°,在坡顶A处测得该塔的塔顶B的仰角为76°.求:

(1)坡顶A到地面PQ的距离;
(2)古塔BC的高度(结果精确到1米).(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为4的正方形ABCD中,P是BC边上一动点(不含B、C两点),将
 ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将
ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将  CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的个数有( ).
CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的个数有( ).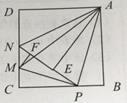
① CMP∽
CMP∽  BPA;
BPA;
②四边形AMCB的面积最大值为10;
③当P为BC中点时,AE为线段NP的中垂线;
④线段AM的最小值为2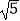 ;
;
⑤当 ABP≌
ABP≌  AND时,BP=4
AND时,BP=4 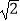 -4.
-4.
A.①②③
B.②③⑤
C.①④⑤
D.①②⑤ -
科目: 来源: 题型:
查看答案和解析>>【题目】如果点P(2x+6,x-4)在平面直角坐标系的第四象限内,那么x的取值范围在数轴上可表示为
A.
 B.
B.  C.
C. 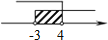 D.
D. 
相关试题

