【题目】如图,在边长为4的正方形ABCD中,P是BC边上一动点(不含B、C两点),将 ![]() ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将
ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将 ![]() CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的个数有( ).
CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的个数有( ).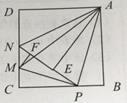
① ![]() CMP∽
CMP∽ ![]() BPA;
BPA;
②四边形AMCB的面积最大值为10;
③当P为BC中点时,AE为线段NP的中垂线;
④线段AM的最小值为2 ![]() ;
;
⑤当 ![]() ABP≌
ABP≌ ![]() AND时,BP=4
AND时,BP=4 ![]() -4.
-4.
A.①②③
B.②③⑤
C.①④⑤
D.①②⑤
参考答案:
【答案】D
【解析】解: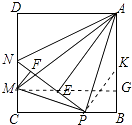 ∵∠APB=∠APE,∠MPC=∠MPN,
∵∠APB=∠APE,∠MPC=∠MPN,
∵∠CPN+∠NPB=180°,
∴2∠NPM+2∠APE=180°,
∴∠MPN+∠APE=90°,
∴∠APM=90°,
∵∠CPM+∠APB=90°,∠APB+∠PAB=90°,
∴∠CPM=∠PAB,
∵四边形ABCD是正方形,
∴AB=CB=DC=AD=4,∠C=∠B=90°,
∴△CMP∽△BPA.故①正确,
设PB=x,则CP=4-x,
∵△CMP∽△BPA,
∴![]() =
=![]() ,
,
∴CM=![]() x(4-x),
x(4-x),
∴S四边形AMCB=![]() [4+
[4+![]() x(4-x)]×4=-
x(4-x)]×4=-![]() x2+2x+8=-
x2+2x+8=-![]() (x-2)2+10,
(x-2)2+10,
∴x=2时,四边形AMCB面积最大值为10,故②正确,
易证得△ADN≌△AEN,当PB=PC=PE=2时,设ND=NE=y,
在RT△PCN中,(y+2)2=(4-y)2+22解得y=![]() ,
,
∴NE≠EP,故③错误,
作MG⊥AB于G,
∵AM=![]() =
=![]() ,
,
∴AG最小时AM最小,
∵AG=AB-BG=AB-CM=4-![]() x(4-x)=
x(4-x)=![]() (x-2)2+3,
(x-2)2+3,
∴x=2时,AG最小值=3,
∴AM的最小值=![]() =5,故④错误.
=5,故④错误.
∵△ABP≌△ADN时,
∴∠PAB=∠DAN=22.5°,在AB上取一点K使得AK=PK,设PB=z,
∴∠KPA=∠KAP=22.5°
∵∠PKB=∠KPA+∠KAP=45°,
∴∠BPK=∠BKP=45°,
∴PB=BK=z,AK=PK=![]() z,
z,
∴z+![]() z=4,
z=4,
∴z=4![]() -4,
-4,
∴PB=4![]() -4,故⑤正确.
-4,故⑤正确.
故正确的为①②⑤.
故选D.
【考点精析】关于本题考查的相似三角形的判定与性质,需要了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校准备购置甲乙两种羽毛球拍若干,已知甲种球拍的单价比乙种球拍的单价多40元,且购买4副甲种球拍与购买6副乙种球拍的费用相同.
(1)两种球拍的单价各是多少元?
(2)若学校准备购买100副甲乙两种羽毛球拍,且购买甲种球拍的费用不少于乙种球拍费用的3倍,问购买多少副甲种球拍总费用最低? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰△ABC的底边长为8cm,腰长为5cm,一动点P在底边上从B向C以0.25cm/s的速度移动,请你探究:当P运动几秒时,P点与顶点A的连线PA与腰垂直。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y=
 (x>0)的图像交矩形OABC的边AB于点D,交边BC于点E,且BE=2EC.若四边形ODBE的面积为6,则k=.
(x>0)的图像交矩形OABC的边AB于点D,交边BC于点E,且BE=2EC.若四边形ODBE的面积为6,则k=.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD顶点A、B在x轴上,点D在y轴上,函数y=
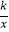 (x>0)的图象经过点C(2,3),直线AD交双曲线于点E,并且EB⊥x轴,CD⊥y轴,EB与CD交于点F.
(x>0)的图象经过点C(2,3),直线AD交双曲线于点E,并且EB⊥x轴,CD⊥y轴,EB与CD交于点F.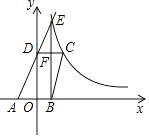
(1)若EB= OD,求点E的坐标;
OD,求点E的坐标;
(2)若四边形ABCD为平行四边形,求过A、D两点的函数关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 ABC中,AD平分
ABC中,AD平分 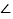 BAC,按如下步骤作图:
BAC,按如下步骤作图:
第一步,分别以点A、D为圆心,以大于 AD的长为半径在AD两侧做弧,交于两点M、N;
AD的长为半径在AD两侧做弧,交于两点M、N;
第二步,连接MN分别交AB、AC于点E、F;
第三步,连接DE、DF.
若BD=6,AF=4,CD=3,则BE的长是( ).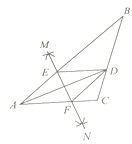
A.2
B.4
C.6
D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax+bx+c的图像如图所示,则代数式(a+b)-c的值( ).

A.大于0
B.等于0
C.小于0
D.不确定
相关试题

