【题目】已知:如图,斜坡AP的坡度为1:2.4,坡长AP为26米,在坡顶A处的同一水平面上有一座古塔BC,在斜坡底P处测得该塔的塔顶B的仰角为45°,在坡顶A处测得该塔的塔顶B的仰角为76°.求:
(1)坡顶A到地面PQ的距离;
(2)古塔BC的高度(结果精确到1米).(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
参考答案:
【答案】
(1)解:过点A作AH⊥PQ,垂足为点H. 
∵斜坡AP的坡度为1:2.4,∴ ![]() =
= ![]() ,
,
设AH=5km,则PH=12km,
由勾股定理,得AP=13km.
∴13k=26m. 解得k=2.
∴AH=10m.
答:坡顶A到地面PQ的距离为10m.
(2)解:延长BC交PQ于点D.
∵BC⊥AC,AC∥PQ,
∴BD⊥PQ.
∴四边形AHDC是矩形,CD=AH=10,AC=DH.
∵∠BPD=45°,
∴PD=BD.
设BC=x,则x+10=24+DH.∴AC=DH=x﹣14.
在Rt△ABC中,tan76°= ![]() ,即
,即 ![]() ≈4.0,
≈4.0,
解得x= ![]() ,即x≈19,
,即x≈19,
答:古塔BC的高度约为19米.
【解析】(1)首先过点A作AH⊥PQ,垂足为H,接下来,依据斜坡AP的坡度为1:2.4,可求得AH,PH,AP的关系,从而可求得AP的长;
(2)设BC=x,首先利用矩形性质求出x+10=24+DH,再利用锐角三角函数的定义列方程求解即可
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,点E、F、H分别是AB、BC、CD的中点,CE、DF交于G,连接AG、HG.下列结论:①CE⊥DF;②AG=AD;③∠CHG=∠DAG;④HG=
 AD.其中正确的有( )
AD.其中正确的有( )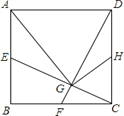
A. ① ② B. ① ② ④ C. ① ③ ④ D. ① ② ③ ④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
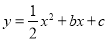 与
与 轴交于
轴交于 和
和 两点,与
两点,与 轴交于
轴交于 点.
点.(1)求此抛物线的解析式;
(2)设
 是线段
是线段 上的动点,作
上的动点,作 交
交 于
于 ,连接
,连接 ,当
,当 的面积是
的面积是 面积的2倍时,求
面积的2倍时,求 点的坐标;
点的坐标;(3)若
 为抛物线上
为抛物线上 、
、 两点间的一个动点,过
两点间的一个动点,过 作
作 轴的平行线,交
轴的平行线,交 于
于 ,当
,当 点运动到什么位置时,线段
点运动到什么位置时,线段 的值最大,并求此时
的值最大,并求此时 点的坐标.
点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题探究
(1)如图1,请在半径为
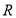 的半圆
的半圆 内(含弧和直径
内(含弧和直径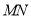 )画出面积最大的三角形,并求出这个三角形的面积;
)画出面积最大的三角形,并求出这个三角形的面积;(2)如图2,请在半径为
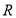 的
的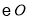 内(含弧)画出面积最大的矩形
内(含弧)画出面积最大的矩形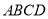 ,并求出这个矩形的面积;
,并求出这个矩形的面积;问题解决
(3)如图3,
 是一块草坪,其中
是一块草坪,其中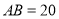 ,
,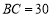 ,
,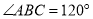 ,某开发商现准备再征一块地,把
,某开发商现准备再征一块地,把 扩充为四边形
扩充为四边形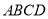 ,使
,使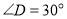 ,是否存在面积最大的四边形
,是否存在面积最大的四边形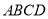 ?若存在,求出四边形
?若存在,求出四边形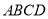 的最大面积;若不存在,请说明理由.(结果保留根号)
的最大面积;若不存在,请说明理由.(结果保留根号)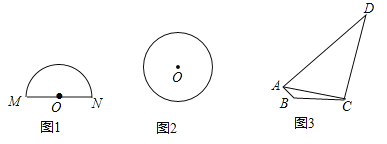
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为4的正方形ABCD中,P是BC边上一动点(不含B、C两点),将
 ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将
ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将  CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的个数有( ).
CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的个数有( ).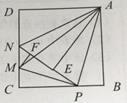
① CMP∽
CMP∽  BPA;
BPA;
②四边形AMCB的面积最大值为10;
③当P为BC中点时,AE为线段NP的中垂线;
④线段AM的最小值为2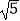 ;
;
⑤当 ABP≌
ABP≌  AND时,BP=4
AND时,BP=4 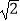 -4.
-4.
A.①②③
B.②③⑤
C.①④⑤
D.①②⑤ -
科目: 来源: 题型:
查看答案和解析>>【题目】如果点P(2x+6,x-4)在平面直角坐标系的第四象限内,那么x的取值范围在数轴上可表示为
A.
 B.
B.  C.
C. 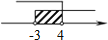 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明做“用频率估计概率”的试验时,根据统计结果,绘制了如图所示的折线统计图,则符合这一结果的试验最有可能的是( )

A. 任意买一张电影票,座位号是2的倍数的概率
B. 一副去掉大小王的扑克牌,洗匀后,从中任抽一张牌的花色是红桃
C. 抛一个质地均匀的正方体骰子,落下后朝上的面点数是3
D. 一个不透明的袋子中有4个白球、1个黑球,它们除了颜色外都相同,从中抽到黑球
相关试题

