【题目】如图,直线![]() ,点
,点![]() 在
在![]() 上,点
上,点![]() 、点
、点![]() 在
在![]() 上,
上,![]() 的角平分线
的角平分线![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,己知
,己知![]() ,则
,则![]() 的度数为( )
的度数为( )
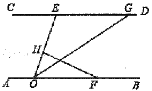
A. 26°B. 32°C. 36°D. 42°
参考答案:
【答案】A
【解析】
依据∠OGD=148°,可得∠EGO=32°,根据AB∥CD,可得∠EGO =∠GOF,根据GO平分∠EOF,可得∠GOE =∠GOF,等量代换可得:∠EGO=∠GOE=∠GOF=32°,根据![]() ,可得:
,可得:![]() =90°-32°-32°=26°
=90°-32°-32°=26°
解:∵ ∠OGD=148°,
∴∠EGO=32°
∵AB∥CD,
∴∠EGO =∠GOF,
∵![]() 的角平分线
的角平分线![]() 交
交![]() 于点
于点![]() ,
,
∴∠GOE =∠GOF,
∵∠EGO=32°
∠EGO =∠GOF
∠GOE =∠GOF,
∴∠GOE=∠GOF=32°,
∵![]() ,
,
∴![]() =90°-32°-32°=26°
=90°-32°-32°=26°
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在长方体
 中,
中, 为平面直角坐标系的原点,
为平面直角坐标系的原点, ,
,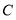 两点的坐标分别为
两点的坐标分别为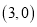 ,
,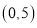 ,点
,点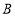 在第一象限.
在第一象限.(1) 写出
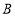 点坐标;
点坐标;(2) 若过点
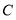 的直线
的直线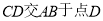 ,且把
,且把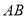 分为
分为 :
: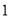 两部分,求出点
两部分,求出点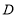 的坐标;
的坐标;(3) 在(2)的条件下,求出四边形
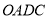 的面积;
的面积;(4) 若点
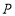 是射线
是射线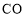 上的点,请直接写出
上的点,请直接写出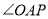 ,
,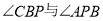 之间的数量关系.
之间的数量关系.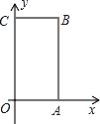
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知锐角三角形ABC内接于⊙O,AD⊥BC,垂足为D.
(1)如图1,
 ,BD=DC,求∠B的度数;
,BD=DC,求∠B的度数;(2)如图2,BE⊥AC,垂足为E,BE交AD于点F,过点B作BG∥AD交⊙O于点G,在AB边上取一点H,使得AH=BG.求证:△AFH是等腰三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=﹣
 +bx+c与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).
+bx+c与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).(1)求抛物线的解析式;
(2)已知点P在抛物线上,连接PC,PB,若△PBC是以BC为直角边的直角三角形,求点P的坐标;
(3)已知点E在x轴上,点F在抛物线上,是否存在以A,C,E,F为顶点的四边形是平行四边形?若存在,请直接写出点E的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列结论中,错误结论有( );①三角形三条高(或高的延长线)的交点不在三角形的内部,就在三角形的外部;②一个多边形的边数每增加一条,这个多边形的内角和就增加360;③两条平行直线被第三条直线所截,同旁内角的角平分线互相平行;④三角形的一个外角等于任意两个内角的和;⑤在
 中,若
中,若 ,则
,则 为直角三角形;⑥顺次延长三角形的三边,所得的三角形三个外角中锐角最多有一个
为直角三角形;⑥顺次延长三角形的三边,所得的三角形三个外角中锐角最多有一个A. 6个B. 5个C. 4个D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形网格中,
 、
、 、
、 均为格点(格点是指每个小正方形的顶点),将
均为格点(格点是指每个小正方形的顶点),将 向下平移6个单位得到
向下平移6个单位得到 .利用网格点和直尺画图:
.利用网格点和直尺画图:
(1)在网格中画出
 ;
;(2)画出
 边上的中线
边上的中线 ,
, 边上的高线
边上的高线 ;
;(3)若
 的边
的边 、
、 分别与
分别与 的边
的边 、
、 垂直,则
垂直,则 的度数是 .
的度数是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①a<0;②
 =1;③b2﹣4ac<0;④当x>1时,y随x的增大而减小;⑤当﹣1<x<3时,y<0,其中正确的是_____.(只填序号)
=1;③b2﹣4ac<0;④当x>1时,y随x的增大而减小;⑤当﹣1<x<3时,y<0,其中正确的是_____.(只填序号)
相关试题

