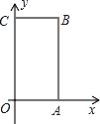
【题目】如图所示,在长方体![]() 中,
中,![]() 为平面直角坐标系的原点,
为平面直角坐标系的原点,![]() ,
,![]() 两点的坐标分别为
两点的坐标分别为![]() ,
,![]() ,点
,点![]() 在第一象限.
在第一象限.
(1) 写出![]() 点坐标;
点坐标;
(2) 若过点![]() 的直线
的直线![]() ,且把
,且把![]() 分为
分为![]() :
:![]() 两部分,求出点
两部分,求出点![]() 的坐标;
的坐标;
(3) 在(2)的条件下,求出四边形![]() 的面积;
的面积;
(4) 若点![]() 是射线
是射线![]() 上的点,请直接写出
上的点,请直接写出![]() ,
,![]() 之间的数量关系.
之间的数量关系.
参考答案:
【答案】(1) 点B的坐标为(3,5);(2) 点D的坐标为(3,4)或(3,1);(3) ![]() 或9;(4) ∠APB=∠CBP+∠OAP或∠APB=∠CBP-∠OAP.
或9;(4) ∠APB=∠CBP+∠OAP或∠APB=∠CBP-∠OAP.
【解析】
(1)根据矩形的性质求出点B的横坐标与纵坐标即可得解;
(2)分AD是4份和1份两种情况讨论求出AD的长,从而得到点D的坐标;
(3)根据梯形的面积公式列式计算即可得解.
(4)分点P在原点上方和在原点下方两种情况求解:连接PB,PA,过点P作PE∥OA,根据平行线的性质可求得结论.
(1)∵A,C两点的坐标分别为(3,0),(0,5),
∴点B的横坐标为3,纵坐标为5,
∴点B的坐标为(3,5);
(2)如图,
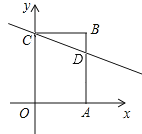
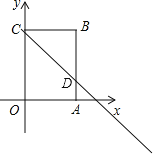
若AD为4份,则AD=5×![]() =4,
=4,
此时点D的坐标为(3,4),
若AD为1份,则AD=5×![]() =1,
=1,
此时点D的坐标为(3,1),
综上所述,点D的坐标为(3,4)或(3,1);
(3)AD=4时,四边形OADC的面积=![]() (4+5)×3=
(4+5)×3=![]() ,
,
AD=1时,四边形OADC的面积=![]() (1+5)×3=9,
(1+5)×3=9,
综上所述,四边形OADC的面积为![]() 或9.
或9.
(4)①当点P在原点上方时,连接PB,PA,过点P作PE∥OA,交AB于点E,如图,
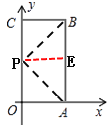
∵四边形OABC是矩形,
∴PE∥BC,
∴∠CBP=∠BPE,∠OAP=∠APE,
∵∠BPE+∠APE=∠CBP+∠OAP,即∠APB=∠CBP+∠OAP.
②当点P在原点下方时,连接PB,PA,过点P作PE∥OA,如图,
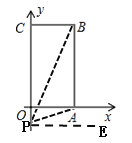
∵四边形OABC是矩形,
∴PE∥BC,
∴∠CBP=∠BPE,∠OAP=∠APE,
∵∠APB=∠BPE-∠APE,
∴∠APB=∠CBP-∠OAP.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某体育用品商店老板到体育商场批发篮球、足球、排球共
 个,得知该体育商场篮球、足球、排球平均每个
个,得知该体育商场篮球、足球、排球平均每个 元,篮球比排球每个多
元,篮球比排球每个多 元,排球比足球每个少
元,排球比足球每个少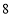 元.
元.(1) 求出这三种球每个各多少元;
(2) 经决定,该老板批发了这三种球的任意两种共
 个,共花费了1060元,问该老板可能买了哪两种球?各买了几个;
个,共花费了1060元,问该老板可能买了哪两种球?各买了几个;(3) 该老板打算将每一种球各提价
 元后,再进行打折销售,若排球、足球打八折,篮球打八五折,在(2)的情况下,为获得最大利润,他批发的一定是哪两种球?各买了几个?计算并说明理由.
元后,再进行打折销售,若排球、足球打八折,篮球打八五折,在(2)的情况下,为获得最大利润,他批发的一定是哪两种球?各买了几个?计算并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分10分)如图,已知直线
 和双曲线
和双曲线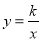 (k>0),点A(m,n)在双曲线
(k>0),点A(m,n)在双曲线  上.当m=n=2时.
上.当m=n=2时.(1)直接写出k的值;
(2)将直线
 作怎样的平移能使平移后的直线与双曲线
作怎样的平移能使平移后的直线与双曲线  只有一个交点.
只有一个交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠A=∠C=45°,∠ADB=∠ABC=105°.
(1)若AD=2,求AB;
(2)若AB+CD=2
 +2,求AB.
+2,求AB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知锐角三角形ABC内接于⊙O,AD⊥BC,垂足为D.
(1)如图1,
 ,BD=DC,求∠B的度数;
,BD=DC,求∠B的度数;(2)如图2,BE⊥AC,垂足为E,BE交AD于点F,过点B作BG∥AD交⊙O于点G,在AB边上取一点H,使得AH=BG.求证:△AFH是等腰三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=﹣
 +bx+c与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).
+bx+c与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).(1)求抛物线的解析式;
(2)已知点P在抛物线上,连接PC,PB,若△PBC是以BC为直角边的直角三角形,求点P的坐标;
(3)已知点E在x轴上,点F在抛物线上,是否存在以A,C,E,F为顶点的四边形是平行四边形?若存在,请直接写出点E的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
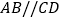 ,点
,点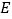 在
在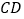 上,点
上,点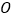 、点
、点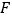 在
在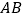 上,
上,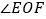 的角平分线
的角平分线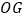 交
交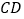 于点
于点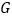 ,过点
,过点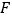 作
作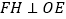 于点
于点 ,己知
,己知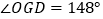 ,则
,则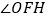 的度数为( )
的度数为( )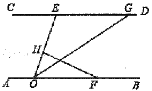
A. 26°B. 32°C. 36°D. 42°
相关试题

