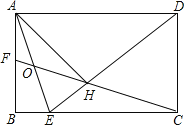
【题目】如图,在矩形ABCD中,![]() ,
,![]() 的平分线交边BC于点E,
的平分线交边BC于点E,![]() 于点H,连接CH并延长交边AB于点F,连接AE交CF于点O,给出下列命题:
于点H,连接CH并延长交边AB于点F,连接AE交CF于点O,给出下列命题:
![]() ,
,![]() ,其中正确命题的序号
,其中正确命题的序号![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】D
【解析】
(1)根据矩形的性质得到AD=BC=![]() AB=
AB=![]() CD,由DE平分∠ADC,得到△ADH是等腰直角三角形,△DEC是等腰直角三角形,得到DE=
CD,由DE平分∠ADC,得到△ADH是等腰直角三角形,△DEC是等腰直角三角形,得到DE=![]() CD,得到等腰三角形DAE,求出∠AED=67.5°,∠AEB=67.5°,得到(1)正确;
CD,得到等腰三角形DAE,求出∠AED=67.5°,∠AEB=67.5°,得到(1)正确;
(2)设DH=1,则AH=DH=1,AD=DE=![]() ,求出HE=
,求出HE=![]() ﹣1,得到2
﹣1,得到2![]() HE≠1,所以(2)不正确;
HE≠1,所以(2)不正确;
(3)通过角的度数求出△AOH和△OEH是等腰三角形,从而得到(3)正确;
(4)由△AFH≌△CHE,到AF=EH,由△ABE≌△AHE,得到BE=EH,于是得到BC﹣BF=(BE+CE)﹣(AB﹣AF)=(CD+EH)﹣(CD﹣EH)=2EH,从而得到(4)不正确.
(1)在矩形ABCD中,AD=BC=![]() AB=
AB=![]() CD,∠ADC=∠BCD=90°.
CD,∠ADC=∠BCD=90°.
∵DE平分∠ADC,∴∠ADE=∠CDE=45°.
∵AH⊥DE,∴△ADH是等腰直角三角形,∴AD=![]() AH,∴AH=AB=CD.
AH,∴AH=AB=CD.
∵△DEC是等腰直角三角形,∴DE=![]() CD,∴AD=DE,∴∠AED=67.5°,∴∠AEB=180°﹣45°﹣67.5°=67.5°,∴∠AEH=∠AEB,所以(1)结论正确;
CD,∴AD=DE,∴∠AED=67.5°,∴∠AEB=180°﹣45°﹣67.5°=67.5°,∴∠AEH=∠AEB,所以(1)结论正确;
(2)设DH=1,则AH=DH=1,AD=DE=![]() ,∴HE=DE﹣DH=
,∴HE=DE﹣DH=![]() ﹣1,∴2
﹣1,∴2![]() HE=2
HE=2![]() (
(![]() ﹣1)=4﹣2
﹣1)=4﹣2![]() ≠1,所以(2)结论不正确;
≠1,所以(2)结论不正确;
(3)∵∠AEH=67.5°,∴∠EAH=22.5°.
∵DH=CD,∠EDC=45°,∴∠DHC=67.5°,∴∠OHA=180°﹣90°﹣67.5°=22.5°,∴∠OAH=∠OHA=22.5°,∴OA=OH,∴∠AEH=∠OHE=67.5°,∴OH=OE=OA,∴OH=![]() AE,所以(3)正确;
AE,所以(3)正确;
(4)∵AH=DH,CD=CE.在△AFH与△CHE中,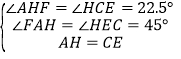 ,∴△AFH≌△CHE,∴AF=EH.在Rt△ABE与Rt△AHE中,
,∴△AFH≌△CHE,∴AF=EH.在Rt△ABE与Rt△AHE中,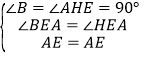 ,∴△ABE≌△AHE,∴BE=EH,∴BC﹣BF=(BE+CE)﹣(AB﹣AF)=(CD+EH)﹣(CD﹣EH)=2EH,所以(4)不正确.
,∴△ABE≌△AHE,∴BE=EH,∴BC﹣BF=(BE+CE)﹣(AB﹣AF)=(CD+EH)﹣(CD﹣EH)=2EH,所以(4)不正确.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点M为矩形ABCD中边BC的中点,若要使
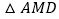 为等腰直角三角形,则再须添加一条件;那么在下列给出的条件中,错误的是
为等腰直角三角形,则再须添加一条件;那么在下列给出的条件中,错误的是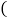
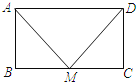
A.
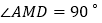 B. AM是
B. AM是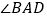 的平分线
的平分线C. AM:
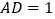 :
: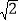 D. AB:
D. AB: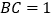 :
:
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等边
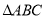 中,点
中,点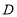 在
在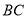 边上,点
边上,点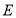 在
在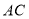 的延长线上,
的延长线上,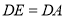 (如图1)
(如图1)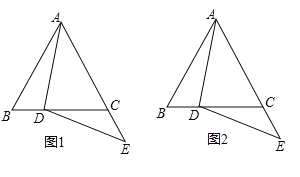
(1)求证:
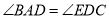 ;
;(2)点
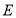 关于直线
关于直线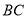 的对称点为
的对称点为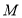 ,连接
,连接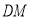 ,
,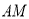 .
.①依题意将图2补全;
②证明:在点
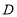 运动的过程中,始终有
运动的过程中,始终有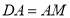 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形
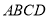 中,
中,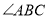 和
和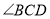 的平分线交于
的平分线交于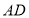 边上一点
边上一点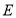 ,且
,且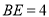 ,
,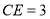 ,则
,则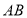 的长是( )
的长是( )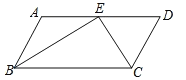
A.3B.4C.5D.2.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,
中, 的角平分线交
的角平分线交 于点
于点 ,点
,点 分
分 为4和5两部分,则
为4和5两部分,则 的周长为( )
的周长为( )A.24B.26C.28D.26或28
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,E、F、G、H分别在它的四条边上,且
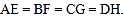 四边形EFGH是什么特殊四边形?你是如何判断的?
四边形EFGH是什么特殊四边形?你是如何判断的?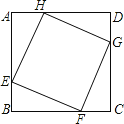
-
科目: 来源: 题型:
查看答案和解析>>【题目】在ABCD中,点E、F分别在AB、CD上,且AE=CF.
(1)求证:△ADE≌△CBF;
(2)若DF=BF,求证:四边形DEBF为菱形.

相关试题

