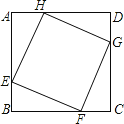
【题目】如图,在正方形ABCD中,E、F、G、H分别在它的四条边上,且![]() 四边形EFGH是什么特殊四边形?你是如何判断的?
四边形EFGH是什么特殊四边形?你是如何判断的?
参考答案:
【答案】四边形![]() 是正方形,理由见解析
是正方形,理由见解析
【解析】
是正方形.可通过证明△AEH,△DHG,△CGF,△BFE全等,先得出四边形EFGH是菱形,再证明四边形EFGH中一个内角为90°,从而得出四边形EFGH是正方形的结论.
四边形EFGH是正方形.
证明:∵AE=BF=CG=GH,∴AH=DG=CF=BE.
∵∠A=∠B=∠C=∠D=90°,∴△AEH≌△DHG≌△CGF≌△BFE,∴EF=EH=HG=GF,∠EHA=∠HGD,∴四边形EFGH是菱形.
∵∠EHA=∠HGD,∠HGD+∠GHD=90°,∴∠EHA+∠GHD=90°,∴∠EHG=90°,∴四边形EFGH是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形
 中,
中, 和
和 的平分线交于
的平分线交于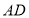 边上一点
边上一点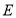 ,且
,且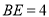 ,
,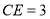 ,则
,则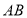 的长是( )
的长是( )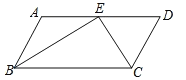
A.3B.4C.5D.2.5
-
科目: 来源: 题型:
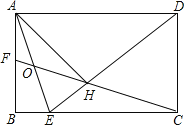
查看答案和解析>>【题目】如图,在矩形ABCD中,
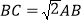 ,
,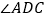 的平分线交边BC于点E,
的平分线交边BC于点E,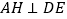 于点H,连接CH并延长交边AB于点F,连接AE交CF于点O,给出下列命题:
于点H,连接CH并延长交边AB于点F,连接AE交CF于点O,给出下列命题: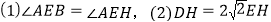 ,
,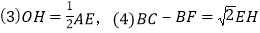 ,其中正确命题的序号
,其中正确命题的序号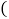
A.
 B.
B.  C.
C. 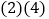 D.
D. 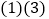
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,
中, 的角平分线交
的角平分线交 于点
于点 ,点
,点 分
分 为4和5两部分,则
为4和5两部分,则 的周长为( )
的周长为( )A.24B.26C.28D.26或28
-
科目: 来源: 题型:
查看答案和解析>>【题目】在ABCD中,点E、F分别在AB、CD上,且AE=CF.
(1)求证:△ADE≌△CBF;
(2)若DF=BF,求证:四边形DEBF为菱形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=
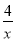 和y=
和y=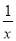 在第一象限内的图象如图,点P是y=
在第一象限内的图象如图,点P是y=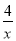 的图象上一动点,PC⊥x轴于点C,交y=
的图象上一动点,PC⊥x轴于点C,交y=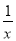 的图象于点B.给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA=
的图象于点B.给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA=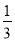 AP.其中所有正确结论的序号是( )
AP.其中所有正确结论的序号是( )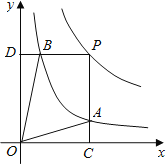
A. ①②③ B. ②③④ C. ①③④ D. ①②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,把直角三角形纸片沿过顶点B的直线(BE交CA于E)折叠,直角顶点C落在斜边AB上,如果折叠后得等腰△EBA,那么结论中:①∠A=30°;②点C与AB的中点重合;③点E到AB的距离等于CE的长,正确的个数是( )
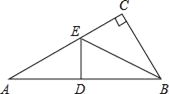
A. 0 B. 1 C. 2 D. 3
相关试题

