【题目】已知,A,B在数轴上对应的数分别用a,b表示,且(![]() ab+100)2+|a﹣20|=0,P是数轴上的一个动点.
ab+100)2+|a﹣20|=0,P是数轴上的一个动点.
(1)在数轴上标出A、B的位置,并求出A、B之间的距离.
(2)已知线段OB上有点C且|BC|=6,当数轴上有点P满足PB=2PC时,求P点对应的数.
(3)动点P从原点开始第一次向左移动1个单位长度,第二次向右移动3个单位长度,第三次向左移动5个单位长度第四次向右移动7个单位长度,….点P能移动到与A或B重合的位置吗?若都不能,请直接回答.若能,请直接指出,第几次移动与哪一点重合?
![]()
参考答案:
【答案】(1)30;(2)P点对应的数为﹣6或2;(3)见解析
【解析】试题分析:(1)先根据非负数的性质求出a,b的值,在数轴上表示出A、B的位置,根据数轴上两点间的距离公式,求出A、B之间的距离即可;
(2)设P点对应的数为x,当P点满足PB=2PC时,分三种情况讨论,根据PB=2PC求出x的值即可;
(3)根据第一次点P表示﹣1,第二次点P表示2,点P表示的数依次为﹣3,4,﹣5,6…,找出规律即可得出结论.
试题解析:解:(1)∵(![]() ab+100)2+|a﹣20|=0,∴
ab+100)2+|a﹣20|=0,∴![]() ab+100=0,a﹣20=0,∴a=20,b=﹣10,∴AB=20﹣(﹣10)=30,数轴上标出A、B得:
ab+100=0,a﹣20=0,∴a=20,b=﹣10,∴AB=20﹣(﹣10)=30,数轴上标出A、B得:
![]()
(2)∵|BC|=6且C在线段OB上,∴xC﹣(﹣10)=6,∴xC=﹣4.∵PB=2PC,当P在点B左侧时PB<PC,此种情况不成立,当P在线段BC上时,xP﹣xB=2(xc﹣xp),∴xp+10=2(﹣4﹣xp),解得:xp=﹣6;
当P在点C右侧时,xp﹣xB=2(xp﹣xc),xp+10=2xp+8,xp=2.
综上所述P点对应的数为﹣6或2.
(3)第一次点P表示﹣1,第二次点P表示2,依次﹣3,4,﹣5,6…
则第n次为(﹣1)nn,点A表示20,则第20次P与A重合;
点B表示﹣10,点P与点B不重合.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB =AC,AD⊥BC于点D,AM是△ABC的外角∠CAE的平分线.
(1)求证:AM∥BC;
(2)若DN平分∠ADC交AM于点N,判断△ADN的形状并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:任意两个数
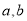 ,按规则
,按规则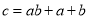 扩充得到一个新数
扩充得到一个新数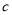 ,称所得的新数
,称所得的新数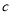 为“如意数”.
为“如意数”.(1)若
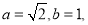 直接写出
直接写出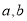 的“如意数”
的“如意数”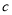 ;
;(2)如果
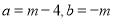 ,求
,求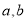 的“如意数”
的“如意数”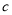 ,并证明“如意数”
,并证明“如意数” 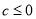 ;
;(3)已知
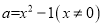 ,且
,且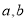 的“如意数”
的“如意数”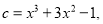 ,则
,则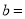 _______________________(用含
_______________________(用含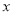 的式子表示)
的式子表示) -
科目: 来源: 题型:
查看答案和解析>>【题目】某开发商进行商铺促销,广告上写着如下条款:投资者购买商铺后,必须由开发商代租赁5年,5年期满后由开发商以比原商铺标价高20%的价格进行回购,投资者可在以下两种购铺方案中做出选择:
方案一:按照商铺标价一次性付清铺款,每年可获得的租金为商铺标价的10%;
方案二:按商铺标价的八折一次性付清铺款,前3年商铺的租金收益归开发商所有,3年后每年可获得的租金为商铺标价的9%
(1)问投资者选择哪种购铺方案,5年后所获得的投资收益率更高?为什么?
(注:投资收益率=
 ×100%)
×100%)(2)对同一标价的商铺,甲选择了购铺方案一,乙选择了购铺方案二,那么5年后两人获得的收益相差7.2万元.问甲乙两人各投资了多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是矩形,点E在AD边上,点F在AD的延长线上,且BE=CF.
(1)求证:四边形EBCF是平行四边形.
(2)若∠BEC=90°,∠ABE=30°,AB=
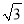 ,求ED的长.
,求ED的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)n边形(n>3)其中一个顶点的对角线有_____条;
(2)一个凸多边形共有14条对角线,它是几边形?
(3)是否存在有21条对角线的凸多边形?如果存在,它是几边形?如果不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地探空气球的气象观测资料表明,高度每增加1千米,气温下降大约5℃,若该地区地面温度为23℃,该地区高空某点温度为-27℃,则此点的高度是大约是多少千米?
相关试题

