【题目】在平面直角坐标系中,现将一块等腰直角三角板ABC放在第二象限,斜靠在两坐上,且点A(0,2),点C(![]() ,0),如图所示:抛物线
,0),如图所示:抛物线![]() 经过点B。
经过点B。

(1)求点B的坐标;
(2)求抛物线的解析式;
(3)在抛物线上是否还存在点P(点B除外),使△ACP仍然是以AC为直角边的等腰直角三角形?若存在,求所有点P的坐标;若不存在,请说明理由。
参考答案:
【答案】(1)(-3,1);(2)y=![]() x2+
x2+![]() x-2;(3)P1(1,-1)、P2(2,1).
x-2;(3)P1(1,-1)、P2(2,1).
【解析】
试题分析:(1)根据题意,过点B作BD⊥x轴,垂足为D;根据角的互余的关系,易得B到x、y轴的距离,即B的坐标;
(2)根据抛物线过B点的坐标,可得a的值,进而可得其解析式;
(3)首先假设存在,分A、C是直角顶点两种情况讨论,根据全等三角形的性质,可得答案.
试题解析:(1)过点B作BD⊥x轴,垂足为D,

∵∠BCD+∠ACO=90°,∠ACO+∠CAO=90°,
∴∠BCD=∠CAO,
又∵∠BDC=∠COA=90°,CB=AC,
∴△BCD≌△CAO,
∴BD=OC=1,CD=OA=2,
∴点B的坐标为(-3,1);
(2)抛物线y=ax2+ax-2经过点B(-3,1),则得到1=9a-3a-2,
解得a=![]() ,
,
所以抛物线的解析式为y=![]() x2+
x2+![]() x-2;
x-2;
(3)假设存在点P,使得△ACP仍然是以AC为直角边的等腰直角三角形:
①若以点C为直角顶点;则延长BC至点P1,使得P1C=BC,得到等腰直角三角形△ACP1,
过点P1作P1M⊥x轴,
∵CP1=BC,∠MCP1=∠BCD,∠P1MC=∠BDC=90°,
∴△MP1C≌△DBC.
∴CM=CD=2,P1M=BD=1,可求得点P1(1,-1);
②若以点A为直角顶点;
则过点A作AP2⊥CA,且使得AP2=AC,得到等腰直角三角形△ACP2,
过点P2作P2N⊥y轴,同理可证△AP2N≌△CAO,
∴NP2=OA=2,AN=OC=1,可求得点P2(2,1),
经检验,点P1(1,-1)与点P2(2,1)都在抛物线y=![]() x2+
x2+![]() x-2上.
x-2上.
考点: 二次函数综合题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂现在平均每天比原计划多生产 50 台机器,现在生产 600 台机器所需时间与原计划生产 450 台机器所需时间相同.
(1)现在平均每天生产多少台机器;
(2)生产 3000 台机器,现在比原计划提前几天完成.
-
科目: 来源: 题型:
查看答案和解析>>【题目】操作:在△ABC中,AC=BC=2,∠C=90°,将一块等腰三角形板的直角顶点放在斜边AB的中点P处,将三角板绕点P旋转,三角板的两直角边分别交射线AC、CB于D、E两点。图①,②,③是旋转三角板得到的图形中的3种情况。研究:
(1)三角板ABC绕点P旋转,观察线段PD和PE之间有什么数量关系?并结合图②加以证明。
(2)三角板ABC绕点P旋转,△PBE是否能为等腰三角形?若能,指出所有情况(即写出△PBE为等腰三角形时CE的长);若不能,请说明理由。(图④不用)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
 与函数
与函数 的图象交于
的图象交于 ,
,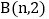 两点,
两点,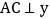 轴于C,
轴于C,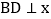 轴于D
轴于D 求k的值;
求k的值;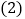 根据图象直接写出
根据图象直接写出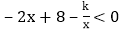 的x的取值范围;
的x的取值范围;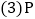 是线段AB上的一点,连接PC,PD,若
是线段AB上的一点,连接PC,PD,若 和
和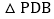 面积相等,求点P坐标.
面积相等,求点P坐标.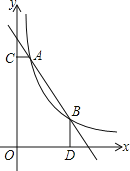
-
科目: 来源: 题型:
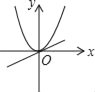
查看答案和解析>>【题目】已知a≠0,在同一直角坐标系中,函数y=ax与y=ax2的图象有可能是( )
A.
 B.
B. 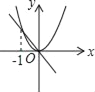 C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年5月14日川航3U863航班挡风玻璃在高空爆裂,机组临危不乱,果断应对.正确处置,顺利返航,避免了一场灾难的发生,下面表格是成都当日海拔高度h(千米)与相应高度处汽温t(℃)的关系(成都地处四川盆地,海拔高度较低,为方便计算,在此题中近似为0米).
海拔高度h(千米)
0
1
2
3
4
5
…
气温t(℃)
20
14
8
2
-4
-1
…
根据上表,回答以下问题:
(1)由上表可知海拔5千米的上空气温约为______℃;
(2)由表格中的规律请写出当日气温t与海拔高度h的关系式为______.
如图是当日飞机下降过程中海拔高度与玻璃爆裂后立即返回地面所用的时间关系图.根据图象回答以下问题:
(3)挡风玻璃在高空爆裂时飞机所处的高度为______千米,返回地面用了______分钟;
(4)飞机在2千米高空水平面上大约盘旋了______分钟;
(5)挡风玻璃在高空爆裂时,当时飞机所处高空的气温为______℃,由此可见机长在高空经历了多大的艰险.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知AB=AC,D为∠BAC的角平分线上面一点,连接BD,CD;如图2,已知AB=AC,D、E为∠BAC的角平分线上面两点,连接BD,CD,BE,CE;如图3,已知AB=AC,D、E、F为∠BAC的角平分线上面三点,连接BD,CD,BE,CE,BF,CF;…,依次规律,第12个图形中有全等三角形的对数是( )
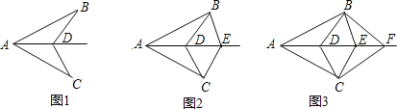
A. 80对B. 78对C. 76对D. 以上都不对
相关试题

