搜索
【题目】如图，在平行四边形ABCD中，连接对角线AC、BD，图中的全等三角形有( )
A. 1对
B. 2对
C. 3对
D. 4对
参考答案：
【答案】D
【解析】
由平行四边形的性质可得：AD=BC，AB=CD，AO=CO，DO=BO，继而结合图形可得△ACD≌△CAB（SSS），△ABD≌△CDB（SSS），△AOD≌△COB（SAS），△AOB≌△COD（SAS），据此即可得答案.
∵四边形ABCD是平行四边形，
∴AB＝CD，AD＝BC；OD＝OB，OA＝OC；
∵在△AOD和△COB中，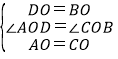
，
∴△AOD≌△COB(SAS)；
同理可得出△AOB≌△COD(SAS)；
∵在△ABD和△DCB中，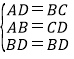
，
∴△ABD≌△CDB(SSS)；
同理可得：△ACD≌△CAB(SSS)，
共有4对全等三角形，
故选D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，△ABC是等腰直角三角形，四边形ADEF是正方形，D，F分别在AB，AC边上，此时BD=CF，BD⊥CF成立．
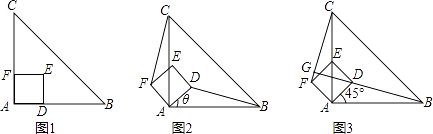
（1）当正方形ADEF绕点A逆时针旋转θ（0°＜θ＜90°）时，如图2，BD=CF成立吗？若成立，请证明；若不成立，请说明理由．
（2）当正方形ADEF绕点A逆时针旋转45°时，如图3，延长BD交CF于点G．求证：BD⊥CF；
（3）在（2）小题的条件下，AC与BG的交点为M，当AB=4，AD=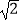
时，求线段CM的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】将一副三角板如图1摆放在直线MN上，在三角板OAB和三角板OCD中，
，
，
．
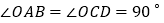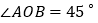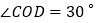保持三角板OCD不动，将三角板OAB绕点O以每秒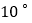
的速度逆时针旋转，旋转时间为t秒．
当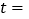
______秒时，OB平分
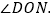此时
______
；
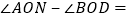当三角板OAB旋转至图2的位置，此时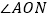
与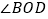
有怎样的数量关系？请说明理由；
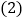如图3，若在三角板OAB开始旋转的同时，另一个三角板OCD也绕点O以每秒
的速度逆时针旋转，当OB旋转至射线OM上时同时停止．当t为何值时，OB平分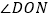
？直接写出在旋转过程中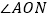，与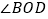之间的数量关系．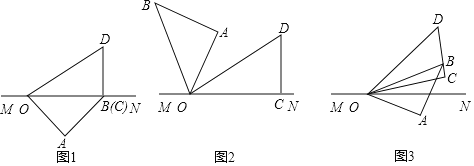
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠ABC＝40°，∠ACD＝76°， BE平分∠ABC，CE平分△ABC的外角∠ACD，则∠E＝（ ）．
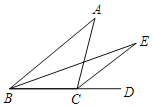
A. 20°B. 36°C. 38°D. 18°
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，矩形ABCD中，点E，F，G，H分别在边AB，BC，CD，DA上，点P在矩形ABCD内．若AB＝4cm，BC＝6cm，AE＝CG＝3cm，BF＝DH＝4cm，四边形AEPH的面积为5cm2，则四边形PFCG的面积为_______cm2．
-
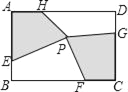
科目： 来源： 题型：
查看答案和解析>>【题目】先化简，再求值：（a﹣2﹣
）÷ 
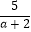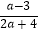，其中a=（3﹣π）0+（ 
）﹣1 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】小明将一副三角板中的两块直角三角尺的直角顶点C按如图所示的方式叠放在一起，当∠ACE＜180°且点E在直线AC的上方时，他发现若∠ACE＝_____，则三角板BCE有一条边与斜边AD平行．（写出所有可能情况）
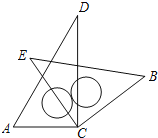
相关试题
