搜索
【题目】如图，在平行四边形ABCD中，点E.F分别在AB、CD上，AE=CF，连接AF，BF，DE，CE，分别交于H、G.
求证：(1)四边形AECF是平行四边形。(2)EF与GH互相平分。
参考答案：
【答案】见解析
【解析】
(1)根据四边形ABCD是平行四边形,由平行四边形的性质可得:
,
,
根据
,利用平行四边形的判定定理可得:四边形AECF是平行四边形,
由
得四边形AECF是平行四边形,根据平行四边形的性质可得:
,
根据,,,可得:
,
,根据平行四边形的判定定理可得:四边形BFDE是平行四边形,再根据平行四边形的性质可得:
,根据平行四边形的判定定理可得:四边形EGFH是平行四边形,由平行四边形的性质可得:
与GH互相平分.
四边形ABCD是平行四边形,
,,
,
四边形AECF是平行四边形,
由得:四边形AECF是平行四边形,
,
,,,
,,
四边形BFDE是平行四边形,
,
四边形EGFH是平行四边形,
与GH互相平分.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线经过点A（﹣1，0）和B（0，2
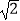），对称轴为x= 
．
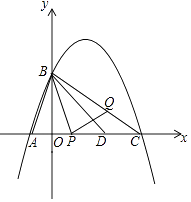
（1）求抛物线的解析式；
（2）抛物线与x轴交于另一个交点为C，点D在线段AC上，已知AD=AB，若动点P从A出发沿线段AC以每秒1个单位长度的度数匀速运动，同时另一动点Q以某一速度从B出发沿线段BC匀速运动，问是否存在某一时刻，使线段PQ被直线BD垂直平分？若存在，求出点Q的运动速度；若不存在，请说明理由．
（3）在（2）的前提下，过点B的直线l与x轴的负半轴交于点M，是否存在点M，使以A，B，M为顶点的三角形与△PBC相似？如果存在，请直接写出M的坐标；若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】某大酒店客房部有三人间、双人间和单人间客房，收费数据如下表（例如三人间普通间客房每人每天收费50元）.为吸引客源，在“十一黄金周”期间进行优惠大酬宾，凡团体入住一律五折优惠.一个50人的旅游团在十月二号到该酒店住宿，租住了一些三人间、双人间普通客房，并且每个客房正好住满，一天一共花去住宿费1510元.
普通间（元/人/天）
豪华间（元/人/天）
贵宾间（元/人/天）
三人间
50
100
500
双人间
70
150
800
单人间
100
200
1500
（1）三人间、双人间普通客房各住了多少间？
（2）设三人间共住了x人，则双人间住了 人，一天一共花去住宿费用y元表示，写出y与x的函数关系式；
（3）如果你作为旅游团团长，你认为上面这种住宿方式是不是费用最少？为什么？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点O为线段AD外一点，M、C、B、N为AD上任意四点，连接OM、OC、OB、ON，下列结论不正确的是（ ）
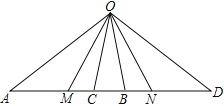
A. 以O为顶点的角共有15个
B. 若OM平分∠AOC，ON平分∠BOD，∠AOD＝5∠COB，则∠MON＝
(∠MOC＋∠BON)C. 若M为AB中点，N为CD中点，则MN＝
(AD－CB)D. 若MC＝CB，MN＝ND，则CD＝2CN
-
科目： 来源： 题型：
查看答案和解析>>【题目】在同一坐标系中，一次函数y=ax+b与二次函数y=bx2+a的图象可能是（ ）
A.
B.
C.
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，边长不等的正方形依次排列，每个正方形都有一个顶点落在函数y=x的图象上，从左向右第3个正方形中的一个顶点A的坐标为（8，4），阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn ， 则Sn的值为 ． （用含n的代数式表示，n为正整数）
-
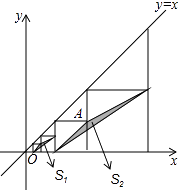
科目： 来源： 题型：
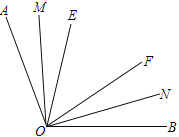
查看答案和解析>>【题目】如图，线段OA绕点O逆时针旋转一周，满足∠EOF始终在∠AOB的内部且∠EOF＝58°．线段OM、ON分别为∠AOE和∠BOF的平分线，在旋转过程中，∠MON的最大值是________.
相关试题
