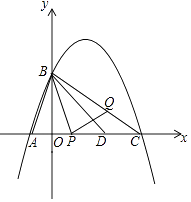
【题目】如图,抛物线经过点A(﹣1,0)和B(0,2 ![]() ),对称轴为x=
),对称轴为x= ![]() .
.
(1)求抛物线的解析式;
(2)抛物线与x轴交于另一个交点为C,点D在线段AC上,已知AD=AB,若动点P从A出发沿线段AC以每秒1个单位长度的度数匀速运动,同时另一动点Q以某一速度从B出发沿线段BC匀速运动,问是否存在某一时刻,使线段PQ被直线BD垂直平分?若存在,求出点Q的运动速度;若不存在,请说明理由.
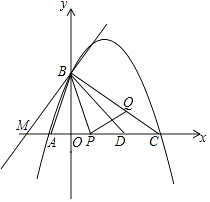
(3)在(2)的前提下,过点B的直线l与x轴的负半轴交于点M,是否存在点M,使以A,B,M为顶点的三角形与△PBC相似?如果存在,请直接写出M的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:设抛物线的解析式为y=a(x﹣ ![]() )2+k,(a≠),
)2+k,(a≠),
把点A(﹣1,0)和B(0,2 ![]() )代入得到
)代入得到 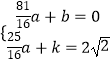 ,
,
解得 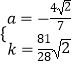 ,
,
∴y=﹣ ![]() (x﹣
(x﹣ ![]() )2+
)2+ ![]() ,
,
∴y=﹣ ![]() x2+
x2+ ![]() x+2
x+2 ![]()
(2)
解:令y=0得到﹣ ![]() x2+
x2+ ![]() x+2
x+2 ![]() =0,解得x=
=0,解得x= ![]() 或﹣1,
或﹣1,
∴C( ![]() ,0),A(﹣1,0),AB=
,0),A(﹣1,0),AB= ![]() =3,
=3,
∵AD=AB,
∴AD=3,
∴D(2,0),
∵PB被BD垂直平分,
∴BP=BQ,
∴∠DBP=∠DBQ,
∴ ![]() (角平分线的性质定理,可以用面积法证明),
(角平分线的性质定理,可以用面积法证明),
∴ ![]() =
= ![]() ,
,
∴t=2或 ![]() ,
,
∵t<3,
∴t=2,
∴BP=3,BQ=3,
∴VQ= ![]()
(3)
解:存在.理由如下:
由题意P(1,0),PB=3,PC= ![]() ,
,
∵BA=BP=2,
∴∠BAP=∠BPA,
∴∠BPC=∠BAM,
①当 ![]() ,△MAB∽△BPC,
,△MAB∽△BPC,
∴ ![]() =
= ![]() ,
,
∴AM= ![]() ,OM=OA+AM=
,OM=OA+AM= ![]()
∴M(﹣ ![]() ,0).
,0).
②当 ![]() 时,△MAB∽CPB,
时,△MAB∽CPB,
∴ ![]() =
= ![]() ,
,
∴AM= ![]() ,OM=AM+OA=
,OM=AM+OA= ![]() ,
,
∴M(﹣ ![]() ,0).
,0).
【解析】(1)设抛物线的解析式为y=a(x﹣ ![]() )2+k,(a≠),把点A(﹣1,0)和B(0,2
)2+k,(a≠),把点A(﹣1,0)和B(0,2 ![]() )代入,解方程组即可解决问题.(2)首先求出A、C坐标,由∠DBP=∠DBQ,可得
)代入,解方程组即可解决问题.(2)首先求出A、C坐标,由∠DBP=∠DBQ,可得 ![]() (角平分线的性质定理,可以用面积法证明),即
(角平分线的性质定理,可以用面积法证明),即 ![]() =
= ![]() ,解方程即可解决问题.(3)存在.理由如下:首先证明∠BPC=∠BAM,分两种情形讨论①当
,解方程即可解决问题.(3)存在.理由如下:首先证明∠BPC=∠BAM,分两种情形讨论①当 ![]() ,△MAB∽△BPC,列出方程解方程即可.②当
,△MAB∽△BPC,列出方程解方程即可.②当 ![]() 时,△MAB∽CPB,列出方程解方程即可.
时,△MAB∽CPB,列出方程解方程即可.
【考点精析】关于本题考查的相似三角形的应用,需要了解测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于一次函数y=x+6,下列结论错误的是( )
A. 函数图象与x轴交点坐标是(0,6) B. 函数值随自变量的增大而增大
C. 函数图象与x轴正方向成45°角 D. 函数图象不经过第四象限
-
科目: 来源: 题型:
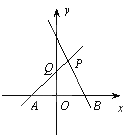
查看答案和解析>>【题目】如图,直线PA是一次函数y=x+1的图象,直线PB是一次函数y=-2x+2的图象.
(1)求A、B、P三点的坐标;
(2)求四边形PQOB的面积;
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明从家骑自行车出发,沿一条直路到相距2400m的邮局办事,小明出发的同时,他的爸爸以96m/min速度从邮局同一条道路步行回家,小明在邮局停留2min后沿原路以原速返回,设他们出发后经过t min时,小明与家之间的距离为s1m,小明爸爸与家之间的距离为s2m,图中折线OABD、线段EF分别表示s1、s2与t之间的函数关系的图象.

(1)求s2与t之间的函数关系式;
(2)小明从家出发,经过多长时间在返回途中追上爸爸?这时他们距离家还有多远?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某大酒店客房部有三人间、双人间和单人间客房,收费数据如下表(例如三人间普通间客房每人每天收费50元).为吸引客源,在“十一黄金周”期间进行优惠大酬宾,凡团体入住一律五折优惠.一个50人的旅游团在十月二号到该酒店住宿,租住了一些三人间、双人间普通客房,并且每个客房正好住满,一天一共花去住宿费1510元.
普通间(元/人/天)
豪华间(元/人/天)
贵宾间(元/人/天)
三人间
50
100
500
双人间
70
150
800
单人间
100
200
1500
(1)三人间、双人间普通客房各住了多少间?
(2)设三人间共住了x人,则双人间住了 人,一天一共花去住宿费用y元表示,写出y与x的函数关系式;
(3)如果你作为旅游团团长,你认为上面这种住宿方式是不是费用最少?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O为线段AD外一点,M、C、B、N为AD上任意四点,连接OM、OC、OB、ON,下列结论不正确的是( )
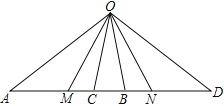
A. 以O为顶点的角共有15个
B. 若OM平分∠AOC,ON平分∠BOD,∠AOD=5∠COB,则∠MON=
 (∠MOC+∠BON)
(∠MOC+∠BON)C. 若M为AB中点,N为CD中点,则MN=
 (AD-CB)
(AD-CB)D. 若MC=CB,MN=ND,则CD=2CN
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点E.F分别在AB、CD上,AE=CF,连接AF,BF,DE,CE,分别交于H、G.
求证:(1)四边形AECF是平行四边形。(2)EF与GH互相平分。

相关试题

