【题目】(本题满分10分)如图,直线y=﹣![]() x+6分别与x轴、y轴交于A、B两点;直线y=
x+6分别与x轴、y轴交于A、B两点;直线y=![]() x与AB交于点C,与过点A且平行于y轴的直线交于点D.点E从点A出发,以每秒1个单位的速度沿x轴向左运动.过点E作x轴的垂线,分别交直线AB、OD于P、Q两点,以PQ为边向右作正方形PQMN.设正方形PQMN与△ACD重叠部分(阴影部分)的面积为S(平方单位),点E的运动时间为t(秒).
x与AB交于点C,与过点A且平行于y轴的直线交于点D.点E从点A出发,以每秒1个单位的速度沿x轴向左运动.过点E作x轴的垂线,分别交直线AB、OD于P、Q两点,以PQ为边向右作正方形PQMN.设正方形PQMN与△ACD重叠部分(阴影部分)的面积为S(平方单位),点E的运动时间为t(秒).
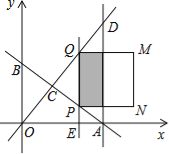
(1)求点C的坐标.
(2)当0<t<5时,求S与t之间的函数关系式,并求S的最大值。
(3)当t>0时,直接写出点(5,3)在正方形PQMN内部时t的取值范围。
参考答案:
【答案】(1)C(3,![]() );(2)S=4t2﹣40t+100,S最大=
);(2)S=4t2﹣40t+100,S最大=![]() ·(3)3<t<4 或 t>7
·(3)3<t<4 或 t>7
【解析】试题分析:(1)解y=﹣![]() x+6与y=
x+6与y=![]() x联立的方程组即可;
x联立的方程组即可;
(2)分别求出0<t≤![]() 时和
时和![]() ≤t<5时的S与t之间的函数关系式,然后利用二次函数的性质求出最大值,比较取大的;(3)点(5,3)在正方形PQMN内部时,点E在x轴上运动,分情况讨论.
≤t<5时的S与t之间的函数关系式,然后利用二次函数的性质求出最大值,比较取大的;(3)点(5,3)在正方形PQMN内部时,点E在x轴上运动,分情况讨论.
试题解析:(1)∵直线y=﹣![]() x+6与直线y=
x+6与直线y=![]() x交于点C,
x交于点C,
∴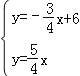 ,解得
,解得![]() ,
,
∴C(3,![]() );
);
(2)∵A点坐标为(8,0),
根据题意,得AE=t,OE=8﹣t
∴点Q的纵坐标为![]() (8﹣t),点P的纵坐标为
(8﹣t),点P的纵坐标为![]() t,
t,
∴PQ=![]() (8﹣t)﹣
(8﹣t)﹣![]() t=10﹣2t.
t=10﹣2t.
当0<t≤![]() 时,S=t(10﹣2t),即S=﹣2t2+10t.当t=
时,S=t(10﹣2t),即S=﹣2t2+10t.当t=![]() 时,S最大=
时,S最大=![]()
当![]() ≤t<5时,S=(10﹣2t)2,即S=4t2﹣40t+100.当t=
≤t<5时,S=(10﹣2t)2,即S=4t2﹣40t+100.当t=![]() 时,S最大=
时,S最大=![]()
∵![]() >
>![]() , ∴S最大=
, ∴S最大=![]()
(3)3<t<4 或 t>7
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠A=∠C=90°,∠ABC=135°,CD=6,AB=2,则四边形ABCD的面积为___________

-
科目: 来源: 题型:
查看答案和解析>>【题目】“十·一”黄金周期间,武汉动物园在7天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
日期
10月1日
10月2日
10月3日
10月4日
10月5日
10月6日
10月7日
人数变化单位:万人
+1.6
+0.8
+0.4
-0.4
-0.8
+0.2
-1.2
(1)若9月30日的游客人数记为
 ,请用
,请用 的代数式表示10月2日的游客人数?
的代数式表示10月2日的游客人数?(2)请判断七天内游客人数最多的是哪天?请说明理由。
(3)若9月30日的游客人数为2万人,门票每人10元。问黄金周期间武汉动物园门票收入是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校开展“青少年科技创新比赛”活动,“喜洋洋”代表队设计了一个遥控车沿直线轨道AC做匀速直线运动的模型.甲、乙两车同时分别从A,B两处出发,沿轨道到达C处,B在AC上,甲的速度是乙的速度的1.5倍,设t(分)后甲、乙两遥控车与B处的距离分别为d1,d2,则d1,d2与t的函数关系如图,试根据图象解决下列问题:
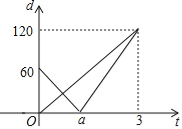
(1)填空:乙的速度v2= 米/分;
(2)写出d1与t的函数关系式:
(3)若甲、乙两遥控车的距离超过10米时信号不会产生相互干扰,试探求什么时间两遥控车的信号不会产生相互干扰?
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)

(2)

(3)
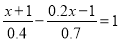
(4)
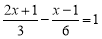
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在等边△ABC中,点D.E分别在边BC,AB上,且BD=AE,AD与CE交于点F.
(1)求证:AD=CE
(2)求∠DFC的度数

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,若点P从点A出发,以每秒2cm的速度沿折线A﹣C﹣B﹣A运动,设运动时间为t秒(t>0).

(1)若点P在AC上,且满足PA=PB时,求出此时t的值;
(2)若点P恰好在∠BAC的角平分线上,求t的值.
相关试题

