搜索
【题目】如图，E是矩形ABCD的边BC上一点，EF⊥AE，EF分别交AC、CD于点M、F，BG⊥AC，垂足为G，BG交AE于点H。
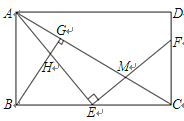
（1）求证：△ABE∽△ECF；
（2）找出与△ABH相似的三角形，并证明；
（3）若E是BC中点，BC=2AB，AB=2，求EM的长。
参考答案：
【答案】（1）证明见解析；（2）
，证明见解析；（3）
【解析】
试题分析：（1）由四边形ABCD是矩形，可得
由
，利用同角的余角相等，可得
，然后利用有两组角对应相等的两个三角形相似，即可证得：
；
由
，易证得
，又由（1）中
，即可证得
；
首先作
，垂足为R，由
，即可求得MR的长，又由
，即可求得答案.
试题解析：（1）
四边形ABCD是矩形，
，
；
（2）.理由：
由（1）知
，
；
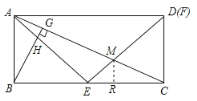
（3）如图所示，作
，垂足为R，由
,
在
中，
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列数据中，哪一组能构成直角三角形（ ）
A.1，2，3
B.5，8，5
C.3，4，5
D.6，8，12 -
科目： 来源： 题型：
查看答案和解析>>【题目】小丽购买学习用品的收据如下表所示，因污损导致部分数据无法识别，根据下表，解决下列问题.
（1）小丽买了自动铅笔、记号笔各几支？
（2）若小丽再次购买软皮笔记本和自动铅笔两种文具，共花费15元，则有哪几种不同的购买方案？
-
科目： 来源： 题型：
查看答案和解析>>【题目】宜兴紧靠太湖，所产百合有“太湖人参”之美誉，今年百合上市后，甲、乙两超市分别用12000元以相同的进价购进质量相同的百合，甲超市销售方案是：将百合按分类包装销售，其中挑出优质的百合400千克，以进价的2倍价格销售，剩下的百合以高于进价10%销售．乙超市的销售方案是：不将百合分类，直接包装销售，价格按甲超市分类销售的两种百合单价和的一半定价．若两超市将百合全部售完，其中甲超市获利8400元（其它成本不计）．问：
（1）百合进价为每千克多少元？
（2）乙超市获利多少元？并比较哪种销售方式更合算．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了预防“流感”，某学校对教室采用药熏消毒法进行消毒，已知药物燃烧时，室内每立方米空气中的含药量y(mg)与时间x(min)成正比例，药物燃烧完后，y与x成反比例（如图所示）。现测得药物8min燃毕，此时室内空气中每立方米的含药量为6mg。研究表明，当空气中每立方米的含药量不低于3mg才有效，那么此次消毒的有效时间是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】在一个不透明的盒子里装有颜色不同的黑、白两种球共40个，小颖做摸球实验，她将盒子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复上述过程，下表是实验中的一组统计数据：
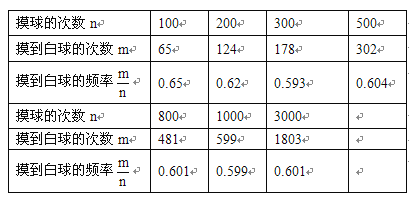
（1）请估计当n很大时，摸到白球的频率将会接近________；(精确到0.1)
（2）假如你摸一次，你摸到白球的概率P(白球)＝________；
（3）试估算盒子里黑、白两种颜色的球各有多少个？
-
科目： 来源： 题型：
查看答案和解析>>【题目】多项式3xy - 5x3y- 4的次数是______,最高次项的系数是______，常数项是______．
相关试题
