【题目】已知Rt△OAB,∠OAB=90°,∠ABO=30°,斜边OB=4,将Rt△OAB绕点O顺时针旋转60°,点D与点A为对应点,画出Rt△ODC,并连接BC.
(1)填空:∠OBC=_____°;
(2)如图,连接AC,作OP⊥AC,垂足为P,求OP的长度是_____.

参考答案:
【答案】(1)60;(2)![]()
【解析】
(1)由旋转得OB=OC,∠BOC=60°,推出△BOC是等边三角形,即可得到答案;
(2)根据已知条件求出OA及AB的长度,利用等边三角形的性质得到BC=4,由此利用勾股定理求出AC=![]() ,过点C作CH⊥AO于点H,则四边形ABCH是矩形,得到CH=AB=
,过点C作CH⊥AO于点H,则四边形ABCH是矩形,得到CH=AB=![]() ,再根据面积法即可求出OP.
,再根据面积法即可求出OP.
(1)由旋转得OB=OC,∠BOC=60°,
∴△BOC是等边三角形,
∴∠OBC=60°,
故答案为:60;
(2)∵∠OAB=90°,∠ABO=30°,OB=4,
∴OA=2,
∴AB=![]() ,
,
∵△BOC是等边三角形,
∴BC=OB=4,
∵∠ABC=∠ABO+∠OBC=90°,
∴![]() ,
,
过点C作CH⊥AO于点H,则四边形ABCH是矩形,
∴CH=AB=![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴OP=![]() ,
,
故答案为:![]() .
.

-
科目: 来源: 题型:
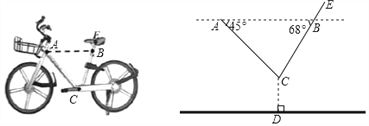
查看答案和解析>>【题目】如图,一辆摩拜单车放在水平的地面上,车把头下方A处与坐垫下方B处在平行于地面的水平线上,A、B之间的距离约为49cm,现测得AC、BC与AB的夹角分别为45°与68°,若点C到地面的距离CD为28cm,坐垫中轴E处与点B的距离BE为4cm,求点E到地面的距离(结果保留一位小数).(参考数据:sin68°≈0.93,cos68°≈0.37,cot68°≈0.40)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a>b,则下列不等式正确的是( )
A.a﹣3>b﹣3B.
 C.﹣3a>﹣3bD.﹣3a+1>﹣3b+1
C.﹣3a>﹣3bD.﹣3a+1>﹣3b+1 -
科目: 来源: 题型:
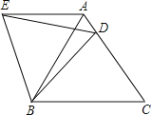
查看答案和解析>>【题目】如图,在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,下列结论正确的有( )个.
①△BED是等边三角形;②AE∥BC; ③△ADE的周长等于BD+BC;④∠ADE=∠DBC.
A.1B.2C.3D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D、E分别在边AB、AC上,DE、BC的延长线相交于点F,且
 .
.(1)求证
 ;
;(2)当AB=12,AC=9,AE=8时,求BD的长与
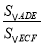 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,抛物线与x轴相交于点A(-2,0)、B(4,0),与y轴交于点C(0,-4),BC与抛物线的对称轴相交于点D.
(1)求该抛物线的表达式,并直接写出点D的坐标;
(2)过点A作AE⊥AC交抛物线于点E,求点E的坐标;
(3)在(2)的条件下,点F在射线AE上,若△ADF∽△ABC,求点F 的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】水池有若干个进水口与出水口,每个口进出水的速度如图1、图2所示,只开1个进水口持续15小时可将水池注满.

(1)某段时间内蓄水量V(m3)与时间t(h)的关系如图3所示,0~3时只开2个进水口,3~b时只开1个进水口与1个出水口,9~c只开1个出水口,求证:a=b+c.
(2)若同时开2个出水口与1个进水口,多久可将满池的水排完?
相关试题

