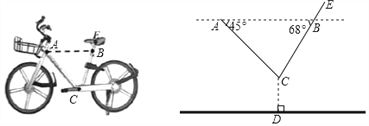
【题目】如图,一辆摩拜单车放在水平的地面上,车把头下方A处与坐垫下方B处在平行于地面的水平线上,A、B之间的距离约为49cm,现测得AC、BC与AB的夹角分别为45°与68°,若点C到地面的距离CD为28cm,坐垫中轴E处与点B的距离BE为4cm,求点E到地面的距离(结果保留一位小数).(参考数据:sin68°≈0.93,cos68°≈0.37,cot68°≈0.40)
参考答案:
【答案】点E到地面的距离约为66.7cm
【解析】分析:过点C作CH⊥AB于H,过点E作EF⊥AB延长线于点F,设CH=x,则AH=CH=x,BH=CHcot68°=0.4x,由AB=49知x+0.4x=49,解之求得CH的长,再由EF=BEsin68°=3.72,根据点E到地面的距离为CH+CD+EF可得答案.
本题解析:过点C作⊥AB于点H,过点E作EF⊥AB延长线于点F,
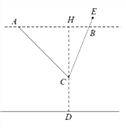
设CH=x,则AH=CH=x, BH=CHcot68°=0.4x,
由AB=49知x+0.4x=49,
解得x=35,∵BE=4,∴EF= BEsin68°=3.72,
则点E到地面的距离为CH+CD+EF=35+28+3.72≈66.7(cm)
答:点E到地面的距离为66.7cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(【材料阅读】阅读下列一段文字,然后回答下列问题.
已知平面内两点M(x1,y1)、N(x2,y2),则这两点间的距离可用下列公式计算:
MN=
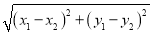 .
.例如:已知P(3,1)、Q(1,﹣2),则这两点间的距离PQ=
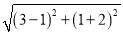 =
=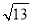 .
.【直接应用】
(1)已知A(2,-3)、B(-4,5),试求A、B两点间的距离;
(2)已知△ABC的顶点坐标分别为A(0,4)、B(﹣1,2)、C(4,2),你能判定△ABC的形状吗?请说明理由.
【深度应用】
(3)如图,在平面直角坐标系xOy中,二次函数y=x2﹣4的图象与x轴相交于两点A、B,(点A在点B的左边)
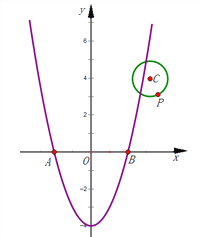
①求点A、B的坐标;
②设点P(m,n)是以点C(3,4)为圆心、1为半径的圆上一动点,求PA2+PB2的最大值;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,点
中,点 是线段
是线段 上一点,
上一点, ,
, .
.
(1)若
 是
是 的高线,且
的高线,且 ,求
,求 的长.
的长.
(2)若
 是
是 的角平分线,
的角平分线, ,求出
,求出 的面积.
的面积.
(3)填空:若
 是
是 的中线,设
的中线,设 长为
长为 ,则
,则 的取值范围______.
的取值范围______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知抛物线
 经过点
经过点 (9,10),交
(9,10),交 轴于点
轴于点 ,直线
,直线 ∥
∥ 轴,点
轴,点 是直线
是直线 下方抛物线上的动点.
下方抛物线上的动点.(1)直接写出抛物线的解析式为 ,点
 的坐标为 、
的坐标为 、 的坐标为 _;
的坐标为 _;(2)过点
 且与
且与 轴平行的直线
轴平行的直线 与直线
与直线 、
、 分别交于点
分别交于点 、
、 ,当四边形
,当四边形 的面积最大时,求
的面积最大时,求 点的坐标;
点的坐标;(3)如图2,当点
 为抛物线的顶点时,在直线
为抛物线的顶点时,在直线 上是否存在点
上是否存在点 ,使得以
,使得以 、
、 、
、 为顶点的三角形与
为顶点的三角形与 相似,若存在,求出点
相似,若存在,求出点 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.


-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a>b,则下列不等式正确的是( )
A.a﹣3>b﹣3B.
 C.﹣3a>﹣3bD.﹣3a+1>﹣3b+1
C.﹣3a>﹣3bD.﹣3a+1>﹣3b+1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,下列结论正确的有( )个.
①△BED是等边三角形;②AE∥BC; ③△ADE的周长等于BD+BC;④∠ADE=∠DBC.
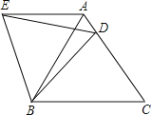
A.1B.2C.3D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知Rt△OAB,∠OAB=90°,∠ABO=30°,斜边OB=4,将Rt△OAB绕点O顺时针旋转60°,点D与点A为对应点,画出Rt△ODC,并连接BC.
(1)填空:∠OBC=_____°;
(2)如图,连接AC,作OP⊥AC,垂足为P,求OP的长度是_____.

相关试题

