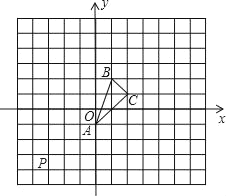
【题目】如图是网格图,每个小正方形的边长均为1.△ABC它在坐标平面内平移,得到△PEF,点A平移后落在点P的位置上.
(1)请你在图中画出△PEF,并写出顶点P、E、F的坐标;
(2)说出△PEF是由△ABC分别经过怎样的平移得到的?
参考答案:
【答案】(1)见解析, P(-3,-3) ,E(-2,0),F(-1,-1);(2) 先向下平移2个单位,再向左平移三个单位;或先向左平移三个单位,再向下平移两个单位
【解析】
(1)根据A点平移到P点的方法,分别找到B、C两点平移后的对应点,再写出坐标即可;
(2)根据图中△ABC和△PEF的位置进行描述即可.
(1)如图所示:
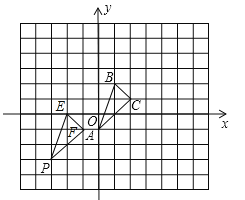
P(-3,-3),E(-2,0),F(-1,-1);
(2)先把△ABC向左平移3个单位长度,再把它向下平移2个单位长度(或先向下平移2个单位长度,再向左平移3个单位长度).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点D是以点A为圆心4为半径的圆上一点,连接BD,点M为BD中点,线段CM长度的最大值为 .
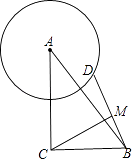
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一元二次方程1﹣(x﹣3)(x+2)=0,有两个实数根x1和x2 , (x1<x2),则下列判断正确的是( )
A.﹣2<x1<x2<3
B.x1<﹣2<3<x2
C.﹣2<x1<3<x2
D.x1<﹣2<x2<3 -
科目: 来源: 题型:
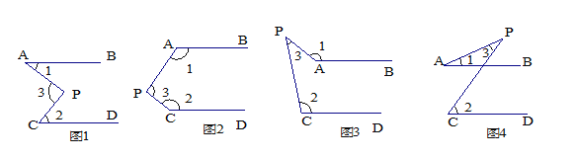
查看答案和解析>>【题目】问题探究:
如下面四个图形中, AB∥CD.
(1)分别说出图1、图2、图3、图4中,∠1与∠2、∠3三者之间的关系.
(2)请你从中任选一个加以说明理由.
解决问题:
(3)如图5所示的是一探照灯灯碗的纵剖面,从位于O点的灯泡发出两束光线OB、OC经灯碗反射后平行射出.如果∠ABO=57°,∠DCO=44°,那么∠BOC=_______°.
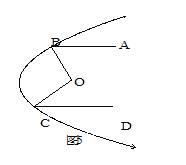
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=﹣x2+mx的图象如图,对称轴为直线x=2,若关于x的一元二次方程﹣x2+mx﹣t=0(t为实数)在1<x<5的范围内有解,则t的取值范围是( )

A.t>﹣5
B.﹣5<t<3
C.3<t≤4
D.﹣5<t≤4 -
科目: 来源: 题型:
查看答案和解析>>【题目】将一幅三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.

(1)求证:CF∥AB.
(2)求∠DFC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学实验室:

制作4张全等的直角三角形纸片(如图1),把这4张纸片拼成以弦长c为边长的正方形构成“弦图”(如图2),古代数学家利用“弦图”验证了勾股定理.
探索研究:
(1)小明将“弦图”中的2个三角形进行了运动变换,得到图3,请利用图3证明勾股定理;
数学思考:
(2)小芳认为用其它的方法改变“弦图”中某些三角形的位置,也可以证明勾股定理.请你想一种方法支持她的观点(先在备用图中补全图形,再予以证明).
相关试题

