【题目】已知点A在数轴上对应的数为a,点B对应的数为b,且|a+4|+(b﹣1)2=0,A、B之间的距离记作|AB|,定义:|AB|=|a﹣b|.
(1)求线段AB的长|AB|;
(2)设点P在数轴上对应的数为x,当|PA|﹣|PB|=2时,求x的值;
(3)若点P在A的左侧,M、N分别是PA、PB的中点,当P在A的左侧移动时,下列两个结论:
①|PM|+|PN|的值不变;②|PN|﹣|PM|的值不变,其中只有一个结论正确,请判断出正确结论,并求其值.
参考答案:
【答案】(1)5;(2)![]() ;(3) ②;
;(3) ②; ![]() .
.
【解析】
试题(1)应用非负数的性质得,a+4=0,b-1=0,解得a和b的值,进而求得|AB|的值;
(2)应考虑到A、B、P三点之间的位置关系的多种可能解题;
(3)当P在A的左侧移动时,设点P对应的数为x,列式求出|PN|-|PM|的值即可.
试题解析:解:(1)由题意得a+4=0,b-1=0,解得a=-4,b=1,所以|AB|=1-(-4)=5;
(2)当P在点A左侧时,|PA|-|PB|=-(|PB|-|PA|)=-|AB|=-5≠2,
当P在点B右侧时,|PA|-|PB|=|AB|=5≠2,
∴上述两种情况的点P不存在,
当P在A、B之间时,|PA|=|x-(-4)|=x+4,|PB|=|x-1|=1-x,
∵|PA|-|PB|=2,∴(x+4)-(1-x)=2,∴x=![]() ;
;
![]() ,
,![]() ,
,![]()
(3)第②个结论正确,|PN|-|PM|=![]() .
.
∵|PN|-|PM|=![]() (|PB|-|PA|)=
(|PB|-|PA|)=![]() |AB|=
|AB|=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有下列函数:①y=
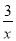 ;②y=
;②y=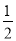 x-1;③y=-3x+1;④y=
x-1;③y=-3x+1;④y=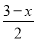 ;⑤y=-
;⑤y=-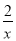 (x>0);⑥y=
(x>0);⑥y=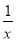 (x<0).其中y随x的增大而减小的是______(填序号).
(x<0).其中y随x的增大而减小的是______(填序号). -
科目: 来源: 题型:
查看答案和解析>>【题目】概念学习
规定:求若干个相同的有理数(均不等于0)的除法运算叫做除方,例如2÷2÷2,(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)等.类比有理数的乘方,我们把2÷2÷2记作2③,读作“2的圈3次方”,(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)记作(﹣3)④,读作“﹣3的圈4次方”,一般地,把
 (a≠0)记作
(a≠0)记作 a
a ,读作“a的圈n次方”.
,读作“a的圈n次方”.初步探究
(1)直接写出计算结果:2③=________,
 =________;
=________;(2)关于除方,下列说法错误的是________
A.任何非零数的圈2次方都等于1; B.对于任何正整数n,1
 =1;
=1; C.3④=4③ ; D.负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数.
深入思考
我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?

(1)试一试:仿照上面的算式,将下列运算结果直接写成幂的形式.
(﹣3)④=________;5⑥=________;
 =________.
=________.(2)想一想:将一个非零有理数a的圈n次方写成幂的形式等于________;
(3)算一算:24÷23+(-16)×2④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列5个结论:
①abc<0;②3a+c>0;③4a+2b+c>0;④2a+b=0;⑤b2>4ac
其中正确的结论的有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列5个结论:
①abc<0;②3a+c>0;③4a+2b+c>0;④2a+b=0;⑤b2>4ac
其中正确的结论的有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=
 x与反比例函数y=
x与反比例函数y=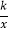 (k>0)的图象交于A,B两点,且点A的横坐标为4.
(k>0)的图象交于A,B两点,且点A的横坐标为4.(1)求k的值.
(2)若反比例函数y=
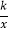 的图象上一点C的纵坐标为8,求△AOC的面积.
的图象上一点C的纵坐标为8,求△AOC的面积.(3)若过原点O的另一条直线l交反比例函数y=
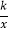 (k>0)的图象于P,Q两点(点P在第一象限),以A,B,P,Q为顶点组成的四边形面积为24,求点P的坐标.
(k>0)的图象于P,Q两点(点P在第一象限),以A,B,P,Q为顶点组成的四边形面积为24,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在纸面上有一数轴(如图),折叠纸面.
(1)若1表示的点与﹣1表示的点重合,则﹣4表示的点与数 _________ 表示的点重合;
(2)若﹣1表示的点与5表示的点重合,回答以下问题:
①13表示的点与数 _________ 表示的点重合;
②若数轴上A、B两点之间的距离为2018(A在B的左侧),且A、B两点经折叠后重合,求A、B两点表示的数是多少?

相关试题

