搜索
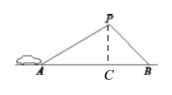
【题目】某条道路上通行车辆限速为60千米/时，在离道路50米处建有一个监测点P，道路AB段为检测区(如图)．在△ABP中，已知∠PAB＝32°，∠PBA＝45°，那么车辆通过AB段的时间在多少秒以内时，可认定为超速？(精确到0.1秒．参考数据：sin32°≈0.53，cos32°≈0.85，tan32°≈0.62)
参考答案：
【答案】7.8秒
【解析】
如下图，过点P作PC⊥AB于点C，由题意可得PC=50米，这样在Rt△PAC和Rt△PBC中分别由已知条件解得AC和BC的长，即可由已知条件求得所求的时间了.
如下图，过点P作PC⊥AB于点C，
∴∠PCA=∠PCB=90°，
∵在Rt△APC中，tan∠PAC＝
，
∴AC＝
≈80.65(米)．
同理，在Rt△PBC中可得：BC＝
＝50(米)．
∴AB＝AC＋BC≈130.65(米)．
∵60千米/时＝
米/秒，则130.65÷≈7.8(秒)．
∴当车辆通过AB段的时间在7.8秒内时，可认定为超速．
-
科目： 来源： 题型：
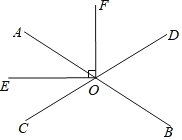
查看答案和解析>>【题目】如图，直线AB、CD相交于点O，OE平分∠AOC，OE⊥OF，∠AOE=32°．
（1）求∠DOB的度数；
（2）OF是∠AOD的角平分线吗？为什么？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，某武警部队在一次地震抢险救灾行动中，探险队员在相距4米的水平地面A，B两处均探测出建筑物下方C处有生命迹象，已知在A处测得探测线与地面的夹角为30°，在B处测得探测线与地面的夹角为60°，求该生命迹象C处与地面的距离．(结果精确到0.1米，参考数据：
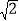≈1.41，
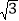≈1.73)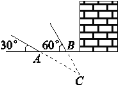
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平行四边形
中，
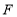是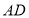
的中点，延长
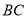到点
，使
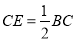，连接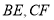
.
（1）求证：四边形
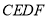是平行四边形；（2）若
，
，
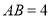，求
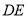的长. -
科目： 来源： 题型：
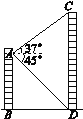
查看答案和解析>>【题目】如图，从楼AB的A处测得对面楼CD的顶部C的仰角为37°，底部D的俯角为45°，两楼的水平距离BD为24 m，那么楼CD的高度约为________ m．(结果精确到1 m，参考数据：sin37°≈0.6，cos37°≈0.8，tan37°≈0.75)
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图是小强洗漱时的侧面示意图，洗漱台(矩形ABCD)靠墙摆放，高AD＝80cm，宽AB＝48cm，小强身高166cm，下半身FG＝100cm，洗漱时下半身与地面成80°(∠FGK＝80°)，身体前倾成125°(∠EFG＝125°)，脚与洗漱台距离GC＝15cm(点D，C，G，K在同一直线上)．
(1)此时小强头部E点与地面DK相距多少？
(2)小强希望他的头部E恰好在洗漱盆AB的中点O的正上方，他应向前或后退多少？
(sin80°≈0.98，cos80°≈0.17，
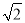≈1.41，结果精确到0.1cm)
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠B=90°，BC=5
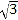，∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动，同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动.设点D、E运动的时间是t秒（t＞0）.过点D作DF⊥BC于点F，连接DE、EF.（1）求证：AE=DF；
（2）四边形AEFD能够成为菱形吗？如果能，求出相应的t值；如果不能，说明理由.
（3）当t为何值时，△DEF为直角三角形？请说明理由.
相关试题
