【题目】如图,某武警部队在一次地震抢险救灾行动中,探险队员在相距4米的水平地面A,B两处均探测出建筑物下方C处有生命迹象,已知在A处测得探测线与地面的夹角为30°,在B处测得探测线与地面的夹角为60°,求该生命迹象C处与地面的距离.(结果精确到0.1米,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
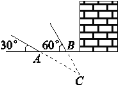
参考答案:
【答案】3.5米
【解析】
如下图,过点C作CD⊥AB,交AB的延长线于点D,结合题意可得∠ADC=90°,∠CAD=30°,∠CBD=60°,这样由三角形外角的性质可得∠ACB=∠CBD-∠CAD=30°=∠CAD,由此可得BC=AB=4米,这样在Rt△CBD中,由sin∠CBD=![]() 即可求得CD的长了.
即可求得CD的长了.
如下图,过点C作CD⊥AB,交AB的延长线于点D,
∴∠ADC=90°,

∵由题意可得:∠CAD=30°,∠CBD=60°,
∴∠CBD-∠CAD=30°,
∴∠CAB=∠ACB=30°,
∴BC=AB=4米.
∵在Rt△CDB中,sin∠CBD=![]() ,
,
∴sin60°=![]() ,
,
∴CD=4sin60°=4×![]() =2
=2![]() ≈3.5(米).
≈3.5(米).
故该生命迹象C处与地面的距离约为3.5米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明、小华在一栋电梯楼前感慨楼房真高.小明说:“这楼起码20层!”小华却不以为然:“20层?我看没有,数数就知道了!”小明说:“有本事,你不用数也能明白!”小华想了想说:“没问题!让我们来量一量吧!”小明、小华在楼体两侧各选A、B两点,测量数据如图,其中矩形CDEF表示楼体,AB=150米,CD=10米,∠A=30°,∠B=45°,(A、C、D、B四点在同一直线上)问:

(1)楼高多少米?
(2)若每层楼按3米计算,你支持小明还是小华的观点呢?请说明理由.(参考数据:
 ≈1.73,
≈1.73,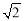 ≈1.41,
≈1.41, ≈2.24)
≈2.24) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,延长AB至E,延长CD至F,BE=DF,连接EF,与BC、AD分别相交于P、Q两点.
(1)求证:CP=AQ;
(2)若BP=1,PQ=
 ,∠AEF=45°,求矩形ABCD的面积.
,∠AEF=45°,求矩形ABCD的面积.
-
科目: 来源: 题型:
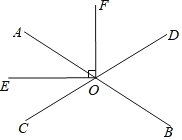
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE平分∠AOC,OE⊥OF,∠AOE=32°.
(1)求∠DOB的度数;
(2)OF是∠AOD的角平分线吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形
 中,
中,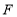 是
是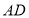 的中点,延长
的中点,延长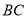 到点
到点 ,使
,使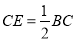 ,连接
,连接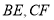 .
.
(1)求证:四边形
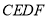 是平行四边形;
是平行四边形;(2)若
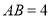 ,
, ,
, ,求
,求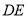 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某条道路上通行车辆限速为60千米/时,在离道路50米处建有一个监测点P,道路AB段为检测区(如图).在△ABP中,已知∠PAB=32°,∠PBA=45°,那么车辆通过AB段的时间在多少秒以内时,可认定为超速?(精确到0.1秒.参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从楼AB的A处测得对面楼CD的顶部C的仰角为37°,底部D的俯角为45°,两楼的水平距离BD为24 m,那么楼CD的高度约为________ m.(结果精确到1 m,参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
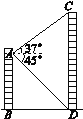
相关试题

