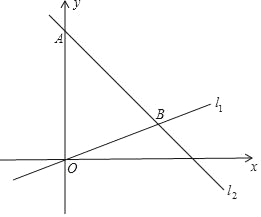
【题目】已知,如图,在平面直角坐标系内,点A的坐标为(0,8),经过原点的直线l1与经过点A的直线l2相交于点B,点B坐标为(6,2).
(1)直接写出直线l1的表达式 ,l2的表达式 ;
(2)点C为线段0B上一动点(点C不与点0,B重合),作CD∥y轴交直线l2于点D,
①设点C的横坐标为3,则点D的坐标为 ;
②设点C的横坐标为m,则点D的坐标为 ;(用含m的代数式表示).
③在②的条件下,若CD=2,则m的值为 .
参考答案:
【答案】(1)y=![]() x;y=﹣x+8;(2)①D(3,5);②D(m,﹣m+8);③
x;y=﹣x+8;(2)①D(3,5);②D(m,﹣m+8);③![]() .
.
【解析】
(1)先设直线l1的表达式为y=k1x,设直线l2的表达式为y=k2x+b,把坐标代入即可求出其解析式;
(2)①②根据点C在直线l1上,把点C的横坐标代入直线l1的表达式即可得出C点坐标,由于CD∥y轴,再根据点D在直线l2上即可得出点D的横坐标,进而得出结论;③根据CD=2列方程即可得到结论.
(1)设直线l1的表达式为y=k1x,它过(6,2)得6k1=2,k1=![]() ,
,
∴y=![]() x;
x;
设直线l2的表达式为y=k2x+b,它过点A(0,8),B(6,2),
得![]() ,
,
解得![]() ,
,
∴直线l2的表达式为:y=﹣x+8;
(2)如图:
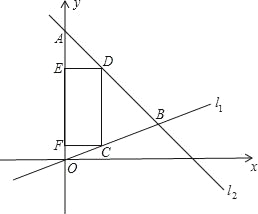
①∵点C在直线l1上,且点C的横坐标为3,
∴y=1,
∴点C的坐标为(3,1),
∵CD∥y轴,
∴点D的横坐标为3,
∵点D在直线l2上,
∴y=﹣3+8=5,
∴D(3,5);
②∵点C在直线l1上,且点C的横坐标为m,
∴y=![]() m,
m,
∴点C的坐标为(m,![]() m),
m),
∵CD∥y轴,
∴点D的横坐标为m,
∵点D在直线l2上,
∴y=﹣m+8,
∴D(m,﹣m+8);
③∵CD=2,
∴﹣m+8﹣![]() m=2,
m=2,
解得:m=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点P是△ABC的边AC上一点.
(1)写出点A、C的坐标:A: ;C:
(2)△ABC的面积为
(3)请在这个坐标系内画出△A1B1C1,使△A1B1C1与△ABC关于y轴对称.
(4)若点P的坐标为(a+1,b﹣1),点P关于y轴的对称点为点Q,则点Q的坐标为 (用含字母a或b的代数式表示)

-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数的图象经过点A(2,1)和点B(0,2).
(1)求出函数的关系式;
(2)在平面置角坐标系内画一次函数的图象,回答下列问题:
①y的值随着x的值的增大而 ,它的图象与x轴的交点坐标是 .
②下列点在一次函数图象上的是 ;
(1,
 ),(﹣2,3),(6,﹣5)
),(﹣2,3),(6,﹣5)③当x ,时,y>0.

-
科目: 来源: 题型:
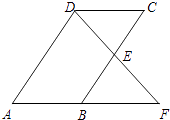
查看答案和解析>>【题目】已知,如图,平行四边形ABCD中,E是BC边的中点,连DE并延长交AB的延长线于点F,求证:AB=BF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题
(1)计算:(﹣1)3﹣( )﹣2×
)﹣2×  +6×|﹣
+6×|﹣  |
|
(2)化简并求值:( )÷
)÷  ,其中a=1,b=2.
,其中a=1,b=2. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙、丁四人玩扑克牌游戏,他们先取出两张红心和两张黑桃共四张扑克牌,洗匀后背面朝上放在桌面上,每人抽取其中一张,拿到相同颜色的即为游戏搭档,现甲、乙两人各抽取了一张,求两人恰好成为游戏搭档的概率.(请用“画树状图”或“列表”等方法写出分析过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形网格中,我们把,每个小正方形的顶点叫做格点,连接任意两个格点的线段叫网格线段,以网格线段为边组成的图形叫做格点图形,在下列如图所示的正方形网格中,每个小正方形的边长为1.
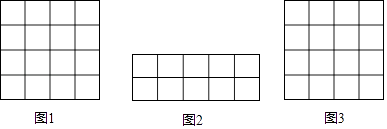
(1)请你在图1中画一个格点图形,且该图形是边长为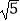 的菱形;
的菱形;
(2)请你在图2中用网格线段将其切割成若干个三角形和正方形,拼接成一个与其面积相等的正方形,并在图3中画出格点正方形.
相关试题

