【题目】如图,在平面直角坐标系中,点P是△ABC的边AC上一点.
(1)写出点A、C的坐标:A: ;C:
(2)△ABC的面积为
(3)请在这个坐标系内画出△A1B1C1,使△A1B1C1与△ABC关于y轴对称.
(4)若点P的坐标为(a+1,b﹣1),点P关于y轴的对称点为点Q,则点Q的坐标为 (用含字母a或b的代数式表示)

参考答案:
【答案】(1)A(﹣3,4),B(﹣4,2);(2)25;(3)详见解析;(4)(﹣a﹣1,b﹣1).
【解析】
(1)直接利用平面直角坐标系得出各点坐标即可;
(2)利用△ABC所在矩形面积减去周围多余三角形的面积进而得出答案;
(3)利用关于y轴对称点的性质得出对应点坐标即可;
(4)利用关于y轴对称点的性质得出对应点坐标即可.
(1)如图所示:

A(﹣3,4),B(﹣4,2);
故答案为:(﹣3,4),(﹣4,2);
(2)△ABC的面积为:2×3﹣![]() ×1×2﹣
×1×2﹣![]() ×1×3﹣
×1×3﹣![]() ×1×2=2.5;
×1×2=2.5;
故答案为:2.5;
(3)如图所示:△A1B1C1,即为所求;
(4)点P的坐标为(a+1,b﹣1),点P关于y轴的对称点为点Q,则点Q的坐标为:(﹣a﹣1,b﹣1).
故答案为:(﹣a﹣1,b﹣1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】水利部确定每年的3月22日至28日为“中国水周”(1994年以前为7月1日至7日),从1991年起,我国还将每年5月的第二周作为城市节约用水宣传周.某社区为了进一步提高居民珍惜水、保护水和水忧患意识,提倡节约用水,从本社区5000户家庭中随机抽取100户,调查他们家庭每月的平均用水量,并将调查的结果绘制成如下的两幅不完整的统计图表:
用户月用水量频数分布表
平均用水量(吨)
频数
频率
3~6吨
10
0.1
6~9吨
m
0.2
9~12吨
36
0.36
12~15吨
25
n
15~18吨
9
0.09

请根据上面的统计图表,解答下列问题:
(1)在频数分布表中:m=__ __,n=__ __;
(2)根据题中数据补全频数直方图;
(3)如果自来水公司将基本月用水量定为每户每月12吨,不超过基本月用水量的部分享受基本价格,超出基本月用水量的部分实行加价收费,那么该社区用户中约有多少户家庭能够全部享受基本价格?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图的正方形方格纸中,每个小的四边形都是相同的正方形,A,B,C,D都在格点处,AB与CD相交于O,则tan∠BOD的值等于 .
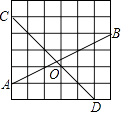
-
科目: 来源: 题型:
查看答案和解析>>【题目】
(1)解不等式组: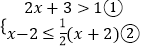
(2)解方程: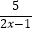 =
= 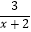 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数的图象经过点A(2,1)和点B(0,2).
(1)求出函数的关系式;
(2)在平面置角坐标系内画一次函数的图象,回答下列问题:
①y的值随着x的值的增大而 ,它的图象与x轴的交点坐标是 .
②下列点在一次函数图象上的是 ;
(1,
 ),(﹣2,3),(6,﹣5)
),(﹣2,3),(6,﹣5)③当x ,时,y>0.

-
科目: 来源: 题型:
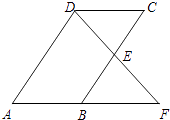
查看答案和解析>>【题目】已知,如图,平行四边形ABCD中,E是BC边的中点,连DE并延长交AB的延长线于点F,求证:AB=BF.
-
科目: 来源: 题型:
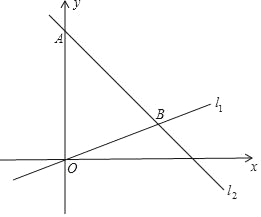
查看答案和解析>>【题目】已知,如图,在平面直角坐标系内,点A的坐标为(0,8),经过原点的直线l1与经过点A的直线l2相交于点B,点B坐标为(6,2).
(1)直接写出直线l1的表达式 ,l2的表达式 ;
(2)点C为线段0B上一动点(点C不与点0,B重合),作CD∥y轴交直线l2于点D,
①设点C的横坐标为3,则点D的坐标为 ;
②设点C的横坐标为m,则点D的坐标为 ;(用含m的代数式表示).
③在②的条件下,若CD=2,则m的值为 .
相关试题

