【题目】数学兴趣小组研究某型号冷柜温度的变化情况,发现该冷柜的工作过程是:当温度达到设定温度![]() ℃时,制冷停止,此后冷柜中的温度开始逐渐上升,当上升到
℃时,制冷停止,此后冷柜中的温度开始逐渐上升,当上升到![]() ℃时,制冷开始,温度开始逐渐下降,当冷柜自动制冷至
℃时,制冷开始,温度开始逐渐下降,当冷柜自动制冷至![]() ℃时,制冷再次停止,…,按照以上方式循环进行.同学们记录
℃时,制冷再次停止,…,按照以上方式循环进行.同学们记录![]() 内9个时间点冷柜中的温度
内9个时间点冷柜中的温度![]() (℃)随时间
(℃)随时间![]() 变化情况,制成下表:
变化情况,制成下表:
时间 | … | 4 | 8 | 10 | 16 | 20 | 21 | 22 | 23 | 24 | … |
温度 | … |
|
|
|
|
|
|
|
|
| … |
(1)如图,在直角坐标系中,描出上表数据对应的点,并画出当![]() 时温度
时温度![]() 随时间
随时间![]() 变化的函数图象;
变化的函数图象;
(2)通过图表分析发现,冷柜中的温度![]() 是时间
是时间![]() 的函数.
的函数.
①当![]() 时,写出符合表中数据的函数解析式;
时,写出符合表中数据的函数解析式;
②当![]() 时,写出符合表中数据的函数解析式;
时,写出符合表中数据的函数解析式;
(3)当前冷柜的温度![]() ℃时,冷柜继续工作36分钟,此时冷柜中的温度是多少?
℃时,冷柜继续工作36分钟,此时冷柜中的温度是多少?
参考答案:
【答案】(1)见详解;(2)①y=![]() ;②y=-4x+76;(3)-4°.
;②y=-4x+76;(3)-4°.
【解析】
(1)根据表格内容描点、画图、连线即可.
(2)①由x·y=-80,即可得出当4≤x<20时,y关于x的函数解析式;
②根据点(20,-4)、(21,-8),利用待定系数法求出y关于x的函数解析式,再代入其它点的坐标验证即可.
(3)根据表格数据,找出冷柜的工作周期为20分钟,由此即可得出答案.
(1)如图所示:
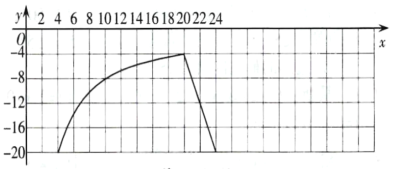
(2)①根据图象可知,图象接近反比例函数图象的一部分,设y=![]() ,过点(8,-10),
,过点(8,-10),
∴k=-80,
∴y=![]() (4≤x<20).
(4≤x<20).
②根据图象可知,图象接近直线,设y=kx+b,过点(20,-4),(21,-8),
∴y=-4x+76.
(3)∵因温度的变化,20分钟一个周期,
∴36=20+16
∴冷柜连续工作36分钟时,在反比例函数变化范围内,故温度为-4°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】课本中有一道作业题:
有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.问加工成的正方形零件的边长是多少mm?
小颖解得此题的答案为48mm,小颖善于反思,她又提出了如下的问题.
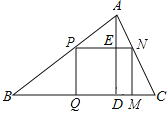
(1)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1,此时,这个矩形零件的两条边长又分别为多少mm?请你计算.
(2)如果原题中所要加工的零件只是一个矩形,如图2,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.
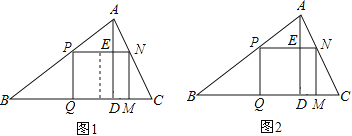
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程
①(x+1)2=4x
②x2+3x﹣4=0(用配方法)
③x2﹣2x﹣8=0
④2(x+4)2=5(x+4)
⑤2x2﹣7x=4
⑥(x+1)(x+2)=2x+4
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个盒中有4个完全相同的小球,把它们分别标号为1,2,3,4,随机摸取一个小球然后放回,再随机摸出一个小球.
(Ⅰ)请用列表法(或画树状图法)列出所有可能的结果;
(Ⅱ)求两次取出的小球标号相同的概率;
(Ⅲ)求两次取出的小球标号的和大于6的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的布袋中装有1个黄球和2个红球,每个球除颜色外都相同.
(1)任意摸出一个球,记下颜色后放回,摇均匀再任意摸出一个球,求两次摸到球的颜色相同的概率;
(2)现将n个蓝球放入布袋,搅匀后任意摸出一个球,记录其颜色后放回,重复该实验.经过大量实验后,发现摸到蓝球的频率稳定于0.7附近,求n的值.
-
科目: 来源: 题型:
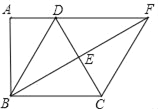
查看答案和解析>>【题目】如图,四边形ABCD中,∠A=90°,AD∥BC,BE⊥CD于E交AD的延长线于F,DC=2AD,AB=BE.
(1)求证:AD=DE.
(2)求证:四边形BCFD是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,△ADE的顶点D,E分别在BC,AC上,且∠DAE=90°,AD=AE.若∠C+∠BAC=145°,则∠EDC的度数为( )

A. 17.5° B. 12.5° C. 12° D. 10°
相关试题

