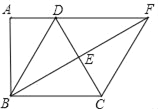
【题目】如图,四边形ABCD中,∠A=90°,AD∥BC,BE⊥CD于E交AD的延长线于F,DC=2AD,AB=BE.
(1)求证:AD=DE.
(2)求证:四边形BCFD是菱形.
参考答案:
【答案】(1)证明见解析,(2)证明见解析.
【解析】
(1)由![]() ,利用“HL”可证△BDA≌△BDE,得出AD=DE;
,利用“HL”可证△BDA≌△BDE,得出AD=DE;
(2)由AD=DE,DC=DE+EC=2AD,可得DE=EC,又AD∥BC,可证△DEF≌△CEB,得出四边形BCFD为平行四边形,再由BE⊥CD证明四边形BCFD是菱形.
证明:(1)∵∠A=∠DEB=90°,
在Rt△BDA与Rt△BDE中,
![]() ,
,
∴△BDA≌△BDE,
∴AD=DE;
(2)∵AD=DE,DC=DE+EC=2AD,
∴DE=EC,
又∵AD∥BC,
∴△DEF≌△CEB,
∴DF=BC,
∴四边形BCFD为平行四边形,
又∵BE⊥CD,
∴四边形BCFD是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个盒中有4个完全相同的小球,把它们分别标号为1,2,3,4,随机摸取一个小球然后放回,再随机摸出一个小球.
(Ⅰ)请用列表法(或画树状图法)列出所有可能的结果;
(Ⅱ)求两次取出的小球标号相同的概率;
(Ⅲ)求两次取出的小球标号的和大于6的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学兴趣小组研究某型号冷柜温度的变化情况,发现该冷柜的工作过程是:当温度达到设定温度
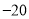 ℃时,制冷停止,此后冷柜中的温度开始逐渐上升,当上升到
℃时,制冷停止,此后冷柜中的温度开始逐渐上升,当上升到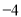 ℃时,制冷开始,温度开始逐渐下降,当冷柜自动制冷至
℃时,制冷开始,温度开始逐渐下降,当冷柜自动制冷至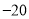 ℃时,制冷再次停止,…,按照以上方式循环进行.同学们记录
℃时,制冷再次停止,…,按照以上方式循环进行.同学们记录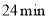 内9个时间点冷柜中的温度
内9个时间点冷柜中的温度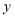 (℃)随时间
(℃)随时间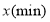 变化情况,制成下表:
变化情况,制成下表:时间
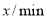
…
4
8
10
16
20
21
22
23
24
…
温度
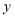 /℃
/℃…
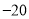
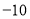
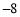
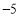
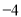
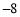
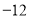
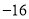
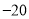
…
(1)如图,在直角坐标系中,描出上表数据对应的点,并画出当
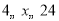 时温度
时温度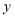 随时间
随时间 变化的函数图象;
变化的函数图象;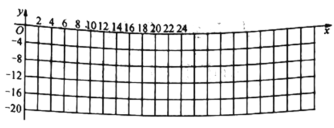
(2)通过图表分析发现,冷柜中的温度
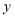 是时间
是时间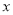 的函数.
的函数.①当
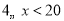 时,写出符合表中数据的函数解析式;
时,写出符合表中数据的函数解析式;②当
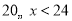 时,写出符合表中数据的函数解析式;
时,写出符合表中数据的函数解析式;(3)当前冷柜的温度
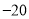 ℃时,冷柜继续工作36分钟,此时冷柜中的温度是多少?
℃时,冷柜继续工作36分钟,此时冷柜中的温度是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的布袋中装有1个黄球和2个红球,每个球除颜色外都相同.
(1)任意摸出一个球,记下颜色后放回,摇均匀再任意摸出一个球,求两次摸到球的颜色相同的概率;
(2)现将n个蓝球放入布袋,搅匀后任意摸出一个球,记录其颜色后放回,重复该实验.经过大量实验后,发现摸到蓝球的频率稳定于0.7附近,求n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,△ADE的顶点D,E分别在BC,AC上,且∠DAE=90°,AD=AE.若∠C+∠BAC=145°,则∠EDC的度数为( )

A. 17.5° B. 12.5° C. 12° D. 10°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+2x+m﹣2=0有两个实数根,m为正整数,且该方程的根都是整数,则符合条件的所有正整数m的和为( )
A. 6 B. 5 C. 4 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线l1:y=﹣
 x+1与x轴,y轴分别交于点A和点B,直线l2:y=kx(k≠0)与直线l1在第一象限交于点C.若∠BOC=∠BCO,则k的值为( )
x+1与x轴,y轴分别交于点A和点B,直线l2:y=kx(k≠0)与直线l1在第一象限交于点C.若∠BOC=∠BCO,则k的值为( )
A.
 B.
B.  C.
C.  D. 2
D. 2
相关试题

