【题目】课本中有一道作业题:
有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.问加工成的正方形零件的边长是多少mm?
小颖解得此题的答案为48mm,小颖善于反思,她又提出了如下的问题.
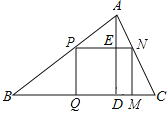
(1)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1,此时,这个矩形零件的两条边长又分别为多少mm?请你计算.
(2)如果原题中所要加工的零件只是一个矩形,如图2,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.
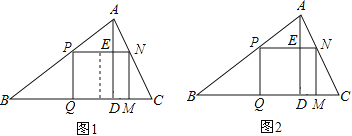
参考答案:
【答案】(1)![]() mm,
mm,![]() mm;(2)PN=60mm,
mm;(2)PN=60mm,![]() mm.
mm.
【解析】
试题(1)、设PQ=y(mm),则PN=2y(mm),AE=80-y(mm),根据平行得出△APN和△ABC相似,根据线段的比值得出y的值,然后得出边长;(2)、根据第一题同样的方法得出y与x的函数关系式,然后求出S与x的函数关系式,根据二次函数的性质得出最大值.
试题解析:(1)、设PQ=y(mm),则PN=2y(mm),AE=80-y(mm)
∵PN∥BC, ∴![]() =
=![]() ,△APN∽△ABC ∴
,△APN∽△ABC ∴![]() =
=![]() ∴
∴![]() =
=![]()
∴![]() =
=![]() 解得 y=
解得 y=![]() ∴2y=
∴2y=![]()
∴这个矩形零件的两条边长分别为![]() mm,
mm,![]() mm
mm
(2)、设PQ=x(mm),PN=y(mm),矩形面积为S ,则AE=80-x(mm)。.
由(1)知![]() =
=![]() ∴
∴![]() =
=![]() ∴ y=
∴ y=![]()
则S=xy=![]() =
=![]() =
=![]()
∵![]() ∴ S有最大值 ∴当x=40时,S最大=2400(mm2) 此时,y=
∴ S有最大值 ∴当x=40时,S最大=2400(mm2) 此时,y=![]() ="60" 。
="60" 。
∴面积达到这个最大值时矩形零件的两边PQ、PN长分别是40 mm ,60 mm。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数
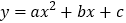 的图象开口向上,图象经过点
的图象开口向上,图象经过点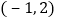 和
和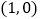 ,且与
,且与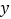 轴相交于负半轴.
轴相交于负半轴.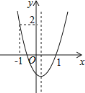
第
 问:给出四个结论:①
问:给出四个结论:① ;②
;② ;③
;③ ;④
;④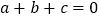 .写出其中正确结论的序号(答对得
.写出其中正确结论的序号(答对得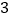 分,少选、错选均不得分)
分,少选、错选均不得分)第
 问:给出四个结论:①abc<0;②2a+b>0;③a+c=1;④a>1.写出其中正确结论的序号.
问:给出四个结论:①abc<0;②2a+b>0;③a+c=1;④a>1.写出其中正确结论的序号. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的顶点A、B的坐标分别为(-4,0)和(2,0),BC=
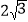 .设直线AC与直线x=4交于点E.
.设直线AC与直线x=4交于点E.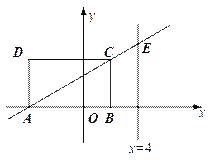
(1)求以直线x=4为对称轴,且过C与原点O的抛物线的函数关系式,并说明此抛物线一定过点E;
(2)设(1)中的抛物线与x轴的另一个交点为N,M是该抛物线上位于C、N之间的一动点,求△CMN面积的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),在
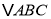 中,
中,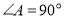 ,
,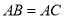 ,点
,点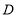 是斜边
是斜边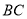 的中点,点
的中点,点 ,
,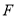 分别在线段
分别在线段 ,
,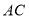 上, 且
上, 且 .
.(1)求证:
 为等腰直角三角形;
为等腰直角三角形;(2)若
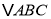 的面积为7,求四边形
的面积为7,求四边形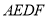 的面积;
的面积;(3)如图(2),如果点
 运动到
运动到 的延长线上时,点
的延长线上时,点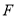 在射线
在射线 上且保持
上且保持 ,
, 还是等腰直角三角形吗.请说明理由.
还是等腰直角三角形吗.请说明理由. 

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在一个边长为1的小正方形组成的方格稿纸上,有A、B、C、D、E、F、G七个点,则在下列任选三个点的方案中可以构成直角三角形的是( )
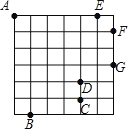
A.点A、点B、点CB.点A、点D、点G
C.点B、点E、点FD.点B、点G、点E
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC三边分别为
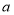 、
、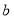 、
、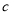 ,根据下列条件能判断△ABC为直角三角形的有 ( )
,根据下列条件能判断△ABC为直角三角形的有 ( ) ①∠A=∠B+∠C;②∠A:∠B:∠C=3:4:5;③
 ;④
;④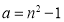 ,
,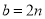 ,
,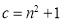
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商人将进货单价为
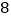 元的某种商品按
元的某种商品按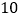 元销售时,每天可卖出
元销售时,每天可卖出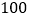 件.现在他采用提高售价的办法增加利润,已知这种商品销售单价每涨
件.现在他采用提高售价的办法增加利润,已知这种商品销售单价每涨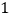 元,销售量就减少
元,销售量就减少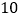 件,那么他将售价每个定为________元时,才能使每天所赚的利润最大,每天最大利润是________元.
件,那么他将售价每个定为________元时,才能使每天所赚的利润最大,每天最大利润是________元.
相关试题

