【题目】如图,要设计一本书的封面,封面长为27cm,宽为21cm,正中央是一个与整个封面长宽比例相同的矩形.如果要使四周的彩色边衬等宽,且四周的彩色边衬所占面积是封面面积的四分之一,应如何设计四周边衬的宽度?(结果保留根号)

封面的长宽之比为27:21=9:7,中央矩形的长宽之比也应是9:7,若设上下边衬的宽均为9xcm,则左右边衬均为7xcm.
(1)用含x的代数式表示:中央矩形的长为______cm,宽为______cm,中央矩形的面积为______cm2.
(2)列出方程并完成本题解答.
参考答案:
【答案】(1)(27-18x);(21-14x);(27-18x)(21-14x);(2)上下边衬的宽为:![]() cm,左右边衬的宽为:
cm,左右边衬的宽为:![]() cm.
cm.
【解析】
(1)设上下边衬的宽均为9xcm,则左右边衬均为7xcm.根据中央矩形的长=封面的长-2×上下边衬的宽,中央矩形的宽=封面的宽-2×左右边衬的宽,再根据矩形的面积=长×宽列式即可;
(2)由于四周的彩色边衬所占面积是封面面积的四分之一,所以中央矩形的面积是封面面积的四分之三,据此列出方程,求解即可.
解:(1)设上下边衬的宽均为9xcm,则左右边衬均为7xcm.
∵一本书的封面长为27cm,宽为21cm,
∴中央矩形的长为(27-18x)cm,宽为(21-14x)cm,中央矩形的面积为(27-18x)(21-14x)cm2.
故答案为(27-18x),(21-14x)cm,(27-18x)(21-14x);
(2)由题意,得(27-18x)(21-14x)=![]() ×27×21,
×27×21,
解得x1=![]() ,x2=
,x2=![]() (不合题意舍去).
(不合题意舍去).
∴上下边衬的宽为:![]() cm,
cm,
左右边衬的宽为:![]() cm.
cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 阅读材料:
为落实水资源管理制度,大力促进水资源节约,本市居民用水实行阶梯水价,按年度用水量计算,将居民家庭全年用水量划分为三档,水价分档递增,实施细则如表:

如某户居民去年用水量为190立方米,则其应缴纳水费为180×5+(190﹣180)×7=970元.
(1)若小明家去年用水量为100立方米,则小明家应缴纳的水费为________元;
(2)若截止10月底,小明家今年共纳水费1145元,则小明家共用水_______立方米;
(3)若小明家全年用水量x不超过270立方米,则应缴纳的水费为多少元?(用含x的代数式表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线AC经过点(1,5)和(-1,1)与直线BC :y = -2x -1相交于点C 。

(1)求直线AC的解析式.
(2)求直AC与y轴交点A的坐标及直线BC与y轴交点B的坐标.
(3)求两直线交点C的坐标.
(4)求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设x、y是任意两个有理数,规定x与y之间的一种运算“⊕”为:
x⊕y=
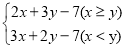
(1)试求1⊕(-1)的值;
(2)试判断该运算“⊕”是否具有交换律,说明你的理由;
(3)若2⊕x=0,求x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图所示,在平面直角坐标系中,四边形ABCO为梯形,BC∥AO,四个顶点坐标分别为A(4,0),B(1,4),C(0,4),O(0,0).一动点P从O出发以每秒1个单位长度的速度沿OA的方向向A运动;同时,动点Q从A出发,以每秒2个单位长度的速度沿A→B→C的方向向C运动.两个动点若其中一个到达终点,另一个也随之停止.设其运动时间为t秒.
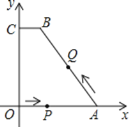
(1)求过A,B,C三点的抛物线的解析式;
(2)当t为何值时,PB与AQ互相平分;
(3)连接PQ,设△PAQ的面积为S,探索S与t的函数关系式.求t为何值时,S有最大值?最大值是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
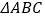 中,
中,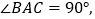
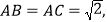
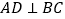 ,垂足为
,垂足为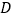 ,过
,过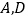 的⊙O分别与
的⊙O分别与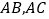 交于点
交于点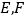 ,连接
,连接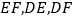 .
.(1)求证:
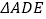 ≌
≌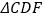 ;
;(2)当
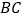 与⊙O相切时,求⊙O的面积.
与⊙O相切时,求⊙O的面积.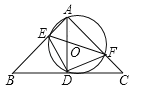
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D,E是△ABC中AB,BC边上的点,且DE∥AC,∠ACB角平分线和它的外角的平分线分别交DE于点G和H.则下列结论错误的是( )
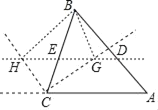
A. 若BG∥CH,则四边形BHCG为矩形
B. 若BE=CE时,四边形BHCG为矩形
C. 若HE=CE,则四边形BHCG为平行四边形
D. 若CH=3,CG=4,则CE=2.5
相关试题

