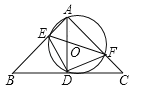
【题目】如图,在![]() 中,
中,![]()
![]()
![]() ,垂足为
,垂足为![]() ,过
,过![]() 的⊙O分别与
的⊙O分别与![]() 交于点
交于点![]() ,连接
,连接![]() .
.
(1)求证:![]() ≌
≌![]() ;
;
(2)当![]() 与⊙O相切时,求⊙O的面积.
与⊙O相切时,求⊙O的面积.
参考答案:
【答案】(1)见解析;(2)![]() .
.
【解析】分析:(1)由等腰直角三角形的性质知AD=CD、∠1=∠C=45°,由∠EAF=90°知EF是⊙O的直径,据此知∠2+∠4=∠3+∠4=90°,得∠2=∠3,利用“ASA”证明即可得;
(2)当BC与⊙O相切时,AD是直径,根据∠C=45°、AC=![]() 可得AD=1,利用圆的面积公式可得答案.
可得AD=1,利用圆的面积公式可得答案.
详解:(1)如图,∵AB=AC,∠BAC=90°,∴∠C=45°.
又∵AD⊥BC,AB=AC,∴∠1=![]() ∠BAC=45°,BD=CD,∠ADC=90°.
∠BAC=45°,BD=CD,∠ADC=90°.
又∵∠BAC=90°,BD=CD,∴AD=CD.
又∵∠EAF=90°,∴EF是⊙O的直径,∴∠EDF=90°,∴∠2+∠4=90°.
又∵∠3+∠4=90°,∴∠2=∠3.在△ADE和△CDF中.
∵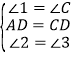 ,∴△ADE≌△CDF(ASA).
,∴△ADE≌△CDF(ASA).
(2)当BC与⊙O相切时,AD是直径.在Rt△ADC中,∠C=45°,AC=![]() ,∴sin∠C=
,∴sin∠C=![]() ,∴AD=ACsin∠C=1,∴⊙O的半径为
,∴AD=ACsin∠C=1,∴⊙O的半径为![]() ,∴⊙O的面积为
,∴⊙O的面积为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设x、y是任意两个有理数,规定x与y之间的一种运算“⊕”为:
x⊕y=
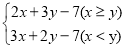
(1)试求1⊕(-1)的值;
(2)试判断该运算“⊕”是否具有交换律,说明你的理由;
(3)若2⊕x=0,求x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,要设计一本书的封面,封面长为27cm,宽为21cm,正中央是一个与整个封面长宽比例相同的矩形.如果要使四周的彩色边衬等宽,且四周的彩色边衬所占面积是封面面积的四分之一,应如何设计四周边衬的宽度?(结果保留根号)

封面的长宽之比为27:21=9:7,中央矩形的长宽之比也应是9:7,若设上下边衬的宽均为9xcm,则左右边衬均为7xcm.
(1)用含x的代数式表示:中央矩形的长为______cm,宽为______cm,中央矩形的面积为______cm2.
(2)列出方程并完成本题解答.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图所示,在平面直角坐标系中,四边形ABCO为梯形,BC∥AO,四个顶点坐标分别为A(4,0),B(1,4),C(0,4),O(0,0).一动点P从O出发以每秒1个单位长度的速度沿OA的方向向A运动;同时,动点Q从A出发,以每秒2个单位长度的速度沿A→B→C的方向向C运动.两个动点若其中一个到达终点,另一个也随之停止.设其运动时间为t秒.
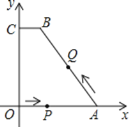
(1)求过A,B,C三点的抛物线的解析式;
(2)当t为何值时,PB与AQ互相平分;
(3)连接PQ,设△PAQ的面积为S,探索S与t的函数关系式.求t为何值时,S有最大值?最大值是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D,E是△ABC中AB,BC边上的点,且DE∥AC,∠ACB角平分线和它的外角的平分线分别交DE于点G和H.则下列结论错误的是( )
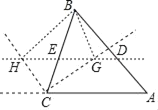
A. 若BG∥CH,则四边形BHCG为矩形
B. 若BE=CE时,四边形BHCG为矩形
C. 若HE=CE,则四边形BHCG为平行四边形
D. 若CH=3,CG=4,则CE=2.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,每个小正方形的边长都为1,四边形ABCD的顶点都在小正方形的顶点上.
(1)求四边形ABCD的面积;
(2)∠BCD是直角吗?说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填入相应的括号里-2,100π,-5
 ,0.8,-|+5.2|,0,0.1010010001…,-(-4
,0.8,-|+5.2|,0,0.1010010001…,-(-4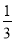 )
)正有理数集合:{ }
整数集合:{ }
负分数集合:{ }
无理数集合:{ }
相关试题

