Question

【题目】已知，如图，直线y=x4与x轴，y轴分别交于B、A，将该直线绕A点顺时针旋转α，且tanα=，旋转后与x轴交于C点．

（1）求A、B、C的坐标；

（2）在x轴上找一点P，使有一动点能在最短的时间内从点A出发，沿着A-P-C的 运动到达C点，并且在AP上以每秒2个单位的速度移动，在PC上以每秒个单位移动，试用尺规作图找到P点的位置（不写作法，保留作图痕迹），并求出所用的最短时间t.

Answer 1

【答案】（1）A(0，4)，B（8，0），C(18，0) ；

（2）作图见解析，t=

【解析】试题分析：（1）过B作BD⊥AB交AC于D，过D作DE⊥x轴于E，则△AOB∽△BED，得到==，求出点D坐标，求出AC的解析式即可求出点C坐标．

（2）过点（0，4）作AC的垂线垂足为Q，该垂线与x轴的交点即为P点．设点F（0，4），则A、F关于x轴对称，所以AP=FP，首先证明t=，由此推出点P就是所求的点，此时动点能在最短的时间内从点A出发，沿着A-P-C的运动到达C点，求出FQ的长即可解决问题．

试题解析：(1)∵直线y=x4与x轴，y轴分别交于B、A，

∴A(0，4)，B(8，0)，

过B作BD⊥AB交AC于D，过D作DE⊥x轴于E，

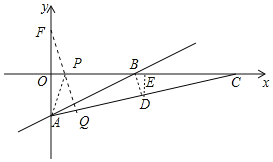
则△AOB∽△BED

∴==，

∵OA=4，OB=8，∠BAD=α，tanα==，

∴BE=1，DE=2

∴D(9，2)

∴直线AC解析式为y=x4

∴C(18，0).

(2)过点(0，4)作AC的垂线垂足为Q，该垂线与x轴的交点即为P点。

设点F(0，4)，则A.F关于x轴对称，所以AP=FP，

S△ACF=AFOC=ACFQ，AF=8，OC=18，AC= ==，

∴FQ=，

∵△CQP∽△COA，

∴，

∴，

∴，

∴t= =，

∵FQ是垂线段，

∴点P就是所求的点，此时动点能在最短的时间内从点A出发，沿着APC的运动到达C点，

∴t=