【题目】有四张背面一模一样的卡片,卡片正面分别写着一个函数关系式,分别是y=2x,y=x2﹣3(x>0),y= ![]() (x>0),y=﹣
(x>0),y=﹣ ![]() (x<0),将卡片顺序打乱后,随意从中抽取一张,取出的卡片上的函数是y随x的增大而增大的概率是( )
(x<0),将卡片顺序打乱后,随意从中抽取一张,取出的卡片上的函数是y随x的增大而增大的概率是( )
A.![]()
B.![]()
C.![]()
D.1
参考答案:
【答案】C
【解析】解:函数y=2x,y=x2﹣3(x>0),y= ![]() (x>0),y=﹣
(x>0),y=﹣ ![]() (x<0)中,有y=2x,y=x2﹣3(x>0),y=﹣
(x<0)中,有y=2x,y=x2﹣3(x>0),y=﹣ ![]() (x<0),是y随x的增大而增大,
(x<0),是y随x的增大而增大,
所以随意从中抽取一张,取出的卡片上的函数是y随x的增大而增大的概率是 ![]() .
.
所以答案是:C.
【考点精析】通过灵活运用正比例函数的图象和性质和反比例函数的性质,掌握正比函数图直线,经过一定过原点.K正一三负二四,变化趋势记心间.K正左低右边高,同大同小向爬山.K负左高右边低,一大另小下山峦;性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△A′B′C′是△ABC 经过平移得到的,△ABC 中任意一点 P(x1,y1)平移后的对应点为 P′(x1+6,y1﹣5).
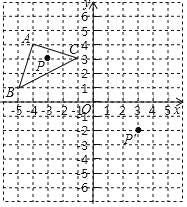
(1)请写出三角形 ABC 平移的过程;
(2)分别写出点 A′,B′,C′的坐标;
(3)画出平移后的图形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个角的两边与另一个角的两边分别平行,结合下图,试探索这两个角之间的数量关系,并说明你的理由.
(1)如图1,AB∥EF,BC∥DE.猜想∠1与∠2的数量关系是:_______.
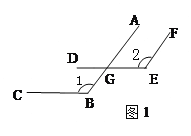
(2)如图2,AB∥EF,BC∥DE. 猜想∠1与∠2的数量关系是:_______.
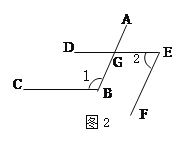
(3)由(1)(2)可以得出的结论是:如果一个角的两边与另一个角的两边分别平行,那么这两个角_____ .
-
科目: 来源: 题型:
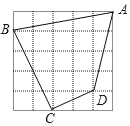
查看答案和解析>>【题目】如图,在5×5的方格纸中,每一个小正方形的边长都为1.
(1)∠BCD是不是直角?请说明理由;
(2)求四边形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图 1,在平面直角坐标系中,点 A 为 x 轴负半轴上一点,点 B 为 x 轴正半轴上一点,C(0,﹣2),D(﹣3,﹣2).


(1)AB,CD 的位置关系为 ;△BCD 的面积为 ;S△ACD S△BCD(填两者之间的数量关系);
(2)如图 1,若∠1=100°,∠ACB=65°,求∠CAB 的度数;
(3)如图 2,若∠ADC=∠DAC,∠ACB 的平分线 CE 交 DA 的延长线于点 E,在 B 点的运动过程中
 的值是否变化?若不变,直接写出其值;若变化,请说明理由.(注:三角形内角和等于 180°)
的值是否变化?若不变,直接写出其值;若变化,请说明理由.(注:三角形内角和等于 180°) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,∠A=90°,点D是BC的中点,点E,F分别在AB,AC上,且∠EDF=90°,连接EF,求证:BE2+CF2=EF2.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线l1∥l2,且l3和l1,l2分别交于A,B两点,点P在AB上.
(1)试找出∠1,∠2,∠3之间的关系并说出理由;
(2)如果点P在A,B两点之间运动,问∠1,∠2,∠3之间的关系是否发生变化?
(3)如果点P在A,B两点外侧运动,试探究∠1,∠2,∠3之间的关系(点P和A,B不重合).

相关试题

