【题目】如图 1,在平面直角坐标系中,点 A 为 x 轴负半轴上一点,点 B 为 x 轴正半轴上一点,C(0,﹣2),D(﹣3,﹣2).


(1)AB,CD 的位置关系为 ;△BCD 的面积为 ;S△ACD S△BCD(填两者之间的数量关系);
(2)如图 1,若∠1=100°,∠ACB=65°,求∠CAB 的度数;
(3)如图 2,若∠ADC=∠DAC,∠ACB 的平分线 CE 交 DA 的延长线于点 E,在 B 点的运动过程中![]() 的值是否变化?若不变,直接写出其值;若变化,请说明理由.(注:三角形内角和等于 180°)
的值是否变化?若不变,直接写出其值;若变化,请说明理由.(注:三角形内角和等于 180°)
参考答案:
【答案】(1)平行,3,=;(2)∠CAB=35°;(3)在B点的运动过程中,∠E与∠ABC的比值不变.![]() .
.
【解析】
(1)根据纵坐标相等的点,所在直线平行于x轴即可得出AB,CD的位置关系,再根据平行线的性质可得△BCD的面积和S△ACD与S△BCD的面积关系;
(2)利用三角形的外角的性质即可解决问题;
(3)设EC交AB于F.∠ADC=∠DAC=α,∠ACE=β,想办法求出∠E,∠ABC(用α,β表示),即可解决问题.
(1)∵C(0,﹣2),D(﹣3,﹣2),
∴CD∥AB,
∴S△BCD=![]() ×3×2=3,S△ACD=S△BCD,
×3×2=3,S△ACD=S△BCD,
故答案为平行,3,=.
(2)如图1中,

∵∠1=180° -∠ABC, ∠CAB+∠ACB=180° -∠ABC,
∴∠1=∠CAB+∠ACB,
∵∠1=100°,∠ACB=65°,
∴∠CAB=100°﹣65°=35°.
(3)在B点的运动过程中,∠E与∠ABC的比值不变.
理由如下:设EC交AB于F.∠ADC=∠DAC=α,∠ACE=β,

在△ACE中,∠E=α﹣β,
在△AFE和△BFC中,∠E+∠EAF+∠AFE=180°,
∠ABC+∠BCF+∠BFC=180°,
∵CD∥x轴,
∴∠EAO=∠ADC,
又∵∠AFE=∠BFC(对顶角相等),
∴∠E+∠EAO=∠ABC+∠BCF,
α﹣β+α=∠ABC+β,
∴∠ABC=2(α﹣β),
∴![]() .
.
即在B点的运动过程中,∠E与∠ABC的比值不变.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个角的两边与另一个角的两边分别平行,结合下图,试探索这两个角之间的数量关系,并说明你的理由.
(1)如图1,AB∥EF,BC∥DE.猜想∠1与∠2的数量关系是:_______.
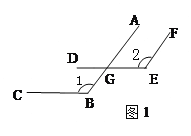
(2)如图2,AB∥EF,BC∥DE. 猜想∠1与∠2的数量关系是:_______.
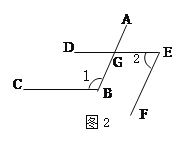
(3)由(1)(2)可以得出的结论是:如果一个角的两边与另一个角的两边分别平行,那么这两个角_____ .
-
科目: 来源: 题型:
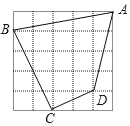
查看答案和解析>>【题目】如图,在5×5的方格纸中,每一个小正方形的边长都为1.
(1)∠BCD是不是直角?请说明理由;
(2)求四边形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有四张背面一模一样的卡片,卡片正面分别写着一个函数关系式,分别是y=2x,y=x2﹣3(x>0),y=
 (x>0),y=﹣
(x>0),y=﹣  (x<0),将卡片顺序打乱后,随意从中抽取一张,取出的卡片上的函数是y随x的增大而增大的概率是( )
(x<0),将卡片顺序打乱后,随意从中抽取一张,取出的卡片上的函数是y随x的增大而增大的概率是( )
A.
B.
C.
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,∠A=90°,点D是BC的中点,点E,F分别在AB,AC上,且∠EDF=90°,连接EF,求证:BE2+CF2=EF2.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线l1∥l2,且l3和l1,l2分别交于A,B两点,点P在AB上.
(1)试找出∠1,∠2,∠3之间的关系并说出理由;
(2)如果点P在A,B两点之间运动,问∠1,∠2,∠3之间的关系是否发生变化?
(3)如果点P在A,B两点外侧运动,试探究∠1,∠2,∠3之间的关系(点P和A,B不重合).

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店进行店庆活动,决定购进甲、乙两种纪念品,若购进甲种纪念品1件,乙种纪念品2件,需要160元;购进甲种纪念品2件,乙种纪念品3件,需要280元.
(1)购进甲乙两种纪念品每件各需要多少元?
(2)该商场决定购进甲乙两种纪念品100件,并且考虑市场需求和资金周转,用于购买这些纪念品的资金不少于6300元,同时又不能超过6430元,则该商场共有几种进货方案?
(3)若销售每件甲种纪念品可获利30元,每件乙种纪念品可获利12元,在第(2)问中的各种进货方案中,哪种方案获利最大?最大利润是多少元?
相关试题

