【题目】如图,△A′B′C′是△ABC 经过平移得到的,△ABC 中任意一点 P(x1,y1)平移后的对应点为 P′(x1+6,y1﹣5).
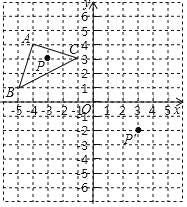
(1)请写出三角形 ABC 平移的过程;
(2)分别写出点 A′,B′,C′的坐标;
(3)画出平移后的图形.
参考答案:
【答案】(1)△ABC向右平移6个单位,向下平移5个单位得到△A′B′C′;(2)A′(2,﹣1),B′(1,﹣4),C′(5,﹣2);(3)如图见解析.
【解析】
(1)根据点的坐标的变化方式可得△ABC的平移方式;
(2)首先确定A、B、C三点坐标,然后每个点的坐标横坐标加6,纵坐标减5即可;
(3)根据(2)中A′,B′,C′的坐标画出图形即可.
解:(1)∵△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1﹣5).
∴△ABC向右平移6个单位,向下平移5个单位得到△A′B′C′;
(2)由图可知A(-4,4)、B(-5,1)、C(-1,3),
所以A′(2,﹣1),B′(1,﹣4),C′(5,﹣2);
(3)如图:
 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线AB交x轴于点A(5,0),交y轴于点B,AO是⊙M的直径,其半圆交AB于点C,且AC=3.取BO的中点D,连接CD、MD和OC.

(1)求证:CD是⊙M的切线;
(2)二次函数的图象经过点D、M、A,其对称轴上有一动点P,连接PD、PM,求△PDM的周长最小时点P的坐标;
(3)在(2)的条件下,当△PDM的周长最小时,抛物线上是否存在点Q,使S△QAM= S△PDM?若存在,求出点Q的坐标;若不存在,请说明理由.
S△PDM?若存在,求出点Q的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是等边三角形ABC内的一点,连结PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连结CQ.若PA∶PB∶PC=3∶4∶5,连结PQ,试判断△PQC的形状( )

A. 直角三角形 B. 等腰三角形 C. 锐角三角形 D. 钝角三角形
-
科目: 来源: 题型:
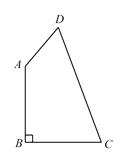
查看答案和解析>>【题目】如图,在四边形ABCD中,∠B=90°,AB=BC=2,AD=1,CD=3.
(1)求∠DAB的度数.
(2)求四边形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个角的两边与另一个角的两边分别平行,结合下图,试探索这两个角之间的数量关系,并说明你的理由.
(1)如图1,AB∥EF,BC∥DE.猜想∠1与∠2的数量关系是:_______.
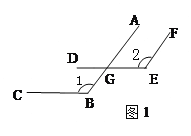
(2)如图2,AB∥EF,BC∥DE. 猜想∠1与∠2的数量关系是:_______.
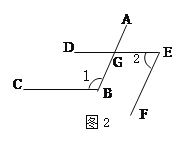
(3)由(1)(2)可以得出的结论是:如果一个角的两边与另一个角的两边分别平行,那么这两个角_____ .
-
科目: 来源: 题型:
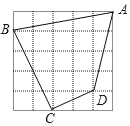
查看答案和解析>>【题目】如图,在5×5的方格纸中,每一个小正方形的边长都为1.
(1)∠BCD是不是直角?请说明理由;
(2)求四边形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有四张背面一模一样的卡片,卡片正面分别写着一个函数关系式,分别是y=2x,y=x2﹣3(x>0),y=
 (x>0),y=﹣
(x>0),y=﹣  (x<0),将卡片顺序打乱后,随意从中抽取一张,取出的卡片上的函数是y随x的增大而增大的概率是( )
(x<0),将卡片顺序打乱后,随意从中抽取一张,取出的卡片上的函数是y随x的增大而增大的概率是( )
A.
B.
C.
D.1
相关试题

