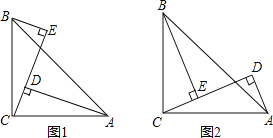
【题目】如图1,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,
(1)△BCE≌△CAD的依据是 (填字母);
(2)猜想:AD、DE、BE的数量关系为 (不需证明);
(3)当BE绕点B、AD绕点A旋转到图2位置时,线段AD、DE、BE之间又有怎样的数量关系,并证明你的结论.
参考答案:
【答案】(1)AAS;(2)见解析;(3)DE=BE﹣AD.
【解析】
试题分析:(1)由题中条件求解△ACD≌△CBE,需要用到两个角和一个边;
(2)由题中条件求解△ACD≌△CBE,得出对应边相等,再利用线段之间的转化,进而可得出结论;
(3)中还是先求解△ACD≌△CBE,利用线段之间的转化得出结论.
(1)解:AAS.
(2)证明:∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
∵AD⊥DE,
∴∠ACD+∠CAD=90°,
∴∠CAD=∠BCE,又AC=BC,
∴△ACD≌△CBE(AAS),
∴AD=CE,BE=CD,
DE=CE﹣CD=AD﹣BE.
(3)解:DE=CD﹣CE=BE﹣AD.
证明:∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
∵AD⊥DE,
∴∠ACD+∠CAD=90°,
∴∠CAD=∠BCE,又AC=BC,
∴△ACD≌△CBE(AAS),∴AD=CE,BE=CD,
DE=CD﹣CE=BE﹣AD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠COA=90°,∠COD比∠DOA大28°,且OB是∠COA的平分线.

(1)求∠BOD的度数;
(2)将已知条件中的28°改为32°,则∠BOD= ;
(3)将已知条件中的28°改为n°,则∠BOD= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在方格纸中,三角形ABC的三个顶点和点P都在小方格的顶点上.

(1)请在图1中,画出将三角形ABC绕点C旋转后的三角形A1B1C,使得点P落在三角形A1B1C内部,且三角形A1B1C的顶点也都落在方格的顶点上.
(2)写出旋转角的度数 .
(3)拓展延伸:如图2,将直角三角形ABC(其中∠C=90°)绕点A按顺时针方向选择115°得到△AB1C1,使得点C,A,B1在同一条直线上,那么∠BAC1等于 .
-
科目: 来源: 题型:
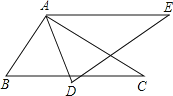
查看答案和解析>>【题目】如图,△ABC≌△ADE,则,AB= ,∠E=∠ .若∠BAE=120°,∠BAD=40°,则∠BAC= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】列运算正确的是( )
A. (﹣3)+(﹣4)=3+(﹣4)= ﹣1
B. (﹣3)+(﹣4)=﹣3+4=1
C. (﹣3)﹣(﹣4)=﹣3+4=1
D. (﹣3)﹣(﹣4)=﹣3﹣4=﹣7
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,AC=BD,∠CAB=∠DBA,试说明:BC=AD

变式1:如图2,AC=BD,BC=AD,试说明:∠CAB=∠DBA;
变式2:如图3,AC=BD,∠C=∠D,试说明:(1)AO=BO(2)CO=DO(3)BC=AD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明计划用100块正方形地板来铺设面积为16m2的客厅,求所需要的一块正方形地板砖的边长.
相关试题

