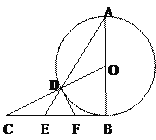
【题目】如图:已知AB是⊙O的直径,BC是⊙O的切线,OC与⊙O相交于点D,连结AD并延长,与BC相交于点E。
(1)若BC=![]() ,CD=1,求⊙O的半径;
,CD=1,求⊙O的半径;
(2)取BE的中点F,连结DF,求证:DF是⊙O的切线。
参考答案:
【答案】(1)解:∵AB是⊙O的直径,BC是⊙O的切线∴AB⊥BC,
设⊙O的半径为![]() ,在Rt△OBC中,∵
,在Rt△OBC中,∵![]()
∴![]() ,解得
,解得![]() =1,∴⊙O的半径为1
=1,∴⊙O的半径为1
(2)连结OF,∵OA=OB,BF=EF,∴OF∥AE,∠A=∠2
又∵∠BOD=2∠A,∴∠1=∠2,
又∵OB=OD、OF=OF∴△OBF≌△ODF,
∴∠ODF=∠OBF=900,即OD⊥DF,∴FD是⊙O的切线。
【解析】(1)先设⊙O的半径为r,由于AB是⊙O的直径,BC是⊙O的切线,根据切线性质可知AB⊥BC,在Rt△OBC中,利用勾股定理可得![]() ,解得r=1;
,解得r=1;
(2)连接OF,由于OA=OB,BF=EF,可知OF是△BAE的中位线,那么OF∥AE,于是∠A=∠2,根据三角形外角性质可得∠BOD=2∠A,易证∠1=∠2,而OD=OB,OF=OF,利用SAS可证△OBF≌△ODF,那么∠ODF=∠OBF=90°,于是OD⊥DF,从而可证FD是⊙O的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴,M为它的顶点
(1)求抛物线的函数关系式;
(2)求△MCB的面积;
(3)设点P是直线l上的一个动点,当PA+PC最小时,求最小值。

-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=mx+n与y=
 ,其中m≠0,n≠0,那么它们在同一坐标系中的图像可能是( )
,其中m≠0,n≠0,那么它们在同一坐标系中的图像可能是( )
A.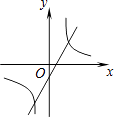
B.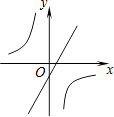
C.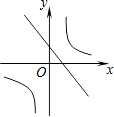
D.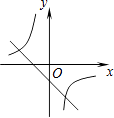
-
科目: 来源: 题型:
查看答案和解析>>【题目】求二次函数y=x2+2x﹣1的对称轴及顶点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班5位学生参加中考体育测试的成绩(单位:分)分别是35、40、37、38、40.则这组数据的众数是( )
A.37
B.40
C.38
D.35 -
科目: 来源: 题型:
查看答案和解析>>【题目】“辽宁号”航母是中国海军航空母舰的首舰,标准排水量57000吨,满载排水量67500吨,数据67500用科学记数法表示为( )
A.675×102
B.67.5×102
C.6.75×104
D.6.75×105 -
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的方程
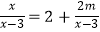 的解是正数,则m的取值范围是 .
的解是正数,则m的取值范围是 .
相关试题

