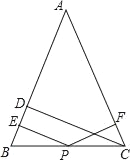
【题目】如图,在△ABC中,AB=AC,CD垂直AB于D,P为BC上的任意一点,过P点分别作PE⊥AB,PF⊥CA,垂足分别为E,F.
(1)若P为BC边中点,则PE,PF,CD三条线段有何数量关系(写出推理过程)?
(2)若P为线段BC上任意一点,则(1)中关系还成立吗?
(3)若P为直线BC上任意一点,则PE,PF,CD三条线段间有何数量关系(请直接写出).
参考答案:
【答案】(1)CD=PE+PF,理由详见解析;(2)成立,理由详见解析;(3)PE﹣PF=CD或PF﹣PE=CD.
【解析】
(1)如图1,连接PA,根据三角形的面积公式列方程即可得到结论;
(2)连接PA,根据三角形的面积公式即可得到结论;
(3)如图2和图3,连接PA,根据三角形的面积列方程即可得到结论.
(1)CD=PE+PF.理由如下:
如图1,连接PA.
∵CD⊥AB于D,PE⊥AB于E,PF⊥AC于F.
∵S△ABC![]() AB×CD,S△PAB
AB×CD,S△PAB![]() AB×PE,S△PAC
AB×PE,S△PAC![]() AC×PF.
AC×PF.
又∵S△ABC=S△PAB+S△PAC,∴![]() AB×CD
AB×CD![]() AB×PE
AB×PE![]() AC×PF.
AC×PF.
∵AB=AC,∴CD=PE+PF.
(2)成立,理由如下:
连接PA.
∵CD⊥AB于D,PE⊥AB于E,PF⊥AC于F.
∵S△ABC![]() AB×CD,S△PAB
AB×CD,S△PAB![]() AB×PE,S△PAC
AB×PE,S△PAC![]() AC×PF.
AC×PF.
又∵S△ABC=S△PAB+S△PAC,∴![]() AB×CD
AB×CD![]() AB×PE
AB×PE![]() AC×PF.
AC×PF.
∵AB=AC,∴CD=PE+PF.
(3)结论:PE﹣PF=CD或PF﹣PE=CD.理由如下:
如图2,连接PA.
∵CD⊥AB于D,PE⊥AB于E,PF⊥AC于F.
∵S△ABC![]() AB×CD,S△PAB
AB×CD,S△PAB![]() AB×PE,S△PAC
AB×PE,S△PAC![]() AC×PF.
AC×PF.
又∵S△ABC=S△PAC﹣S△PAB,∴![]() AB×CD
AB×CD![]() AC×PF
AC×PF![]() AB×PE.
AB×PE.
∵AB=AC,∴CD=PF﹣PE.
如图3,连接PA.
∵CD⊥AB于D,PE⊥AB于E,PF⊥AC于F.
∵S△ABC![]() AB×CD,S△PAB
AB×CD,S△PAB![]() AB×PE,S△PAC
AB×PE,S△PAC![]() AC×PF.
AC×PF.
又∵S△ABC=S△PAB﹣S△PAC,∴![]() AB×CD
AB×CD![]() AB×PE
AB×PE![]() AC×PF.
AC×PF.
∵AB=AC,∴CD=PE﹣PF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如下图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=
 a°,则下列结论: ①∠BOE=
a°,则下列结论: ①∠BOE= (180-a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确的个数有( )个.
(180-a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确的个数有( )个.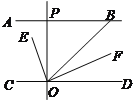
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
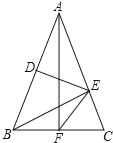
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,DE垂直平分AB.若BE⊥AC,AF⊥BC,垂足分别为点E,F,连接EF,则∠EFC=_____.
-
科目: 来源: 题型:
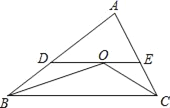
查看答案和解析>>【题目】如图,△ABC中,点O是∠BCA与∠ABC的平分线的交点,过O作与BC平行的直线分别交AB、AC于D、E.已知△ABC的周长为15,BC的长为6,求△ADE的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,CD相交于O点,OM⊥AB.
(1)若∠1=∠2,求∠NOD;
(2)若∠1=
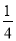 ∠BOC,求∠AOC与∠MOD.
∠BOC,求∠AOC与∠MOD. 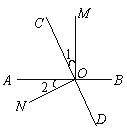
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列几何体是由4个相同的小正方体搭成的,其中主视图和左视图相同的是( )
A.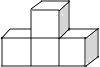
B.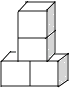
C.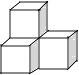
D.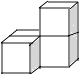
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC的周长是20,OB和OC分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=3,则△ABC的面积是( )
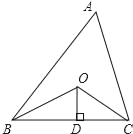
A. 20 B. 25 C. 30 D. 35
相关试题

