【题目】如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点.点P是直径MN上一动点,则PA+PB的最小值为( )

A. ![]() B. 1 C. 2 D.
B. 1 C. 2 D. ![]()
参考答案:
【答案】A
【解析】试题解析:作点B关于MN的对称点B′,连接OA、OB、OB′、AB′,
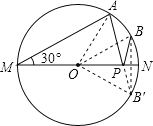
则AB′与MN的交点即为PA+PB的最小时的点,PA+PB的最小值=AB′,
∵∠AMN=30°,
∴∠AON=2∠AMN=2×30°=60°,
∵点B为劣弧AN的中点,
∴∠BON=![]() ∠AON=
∠AON=![]() ×60°=30°,
×60°=30°,
由对称性,∠B′ON=∠BON=30°,
∴∠AOB′=∠AON+∠B′ON=60°+30°=90°,
∴△AOB′是等腰直角三角形,
∴AB′=![]() OA=
OA=![]() ×1=
×1=![]() ,
,
即PA+PB的最小值=![]() .
.
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E为ABCD边AD上一点,将△ABE沿BE翻折得到△FBE,点F在BD上,且EF=DF,若∠BDC=81°,则∠C=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某一出租车一天下午以鼓楼为出发点在东西方向运营,向东走为正,向西走为负,行车里程(单位:km)依先后次序记录如下:
 .
.(1)将最后一名乘客送到目的地,出租车离鼓楼出发点多远?在鼓楼的什么方向?
(2)若每千米的价格为2.4元,司机一个下午的营业额是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B是双曲线
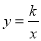 上的点,点A的坐标是
上的点,点A的坐标是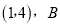 是线段AC的中点.
是线段AC的中点.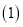 求k的值;
求k的值;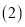 求点B的坐标;
求点B的坐标;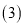 求
求 的面积.
的面积.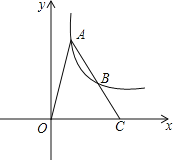
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(-8)+10-2+(-1); (2)12-7×(-4)+8÷(-2);
(3)(
 )÷(-
)÷(- ); (4)-14-(1+0.5)×
); (4)-14-(1+0.5)× ÷(-4)2.
÷(-4)2. -
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填入相应的集合内:
4.2 , 50% , 0 , ,
 , 2.122222…, 3.01001…,
, 2.122222…, 3.01001…, ,
,  ,
, 
正数集合:{ };
分数集合:{ };
负有理数集合:{ };
无理数集合:{ }.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图, ⊙O 的半径是2,直线l与⊙O 相交于A、B 两点,M、N 是⊙O 上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB 面积的最大值是 .

相关试题

