【题目】一只不透明的袋子中有3个红球,3个绿球和若干个白球,每个球除颜色外都相同,将球搅匀,从中任意摸出一个球.
(1)若袋子内白球有4个,任意摸出一个球是绿球的概率是多少?
(2)如果任意摸出一个球是绿球的概率是![]() ,求袋子内有几个白球?
,求袋子内有几个白球?
参考答案:
【答案】(1)![]() ;(2)6个
;(2)6个
【解析】分析:(1)由题意可知,任意摸出一个球总共有10种结果,摸出的球为绿球的结果有3种,根据概率公式即可得答案;(2)设袋子内有x个白球,根据概率公式列出方程,解方程即可求得袋子内白球的个数.
详解:
(1)一只不透明的袋子中有3个红球,3个绿球和白球有4个,一只不透明的袋子中一共有10个球,任意摸出一个球是绿球的概率是![]() .
.
(2)任意摸出一个球是绿球的概率是![]() ,设袋子内有x个白球,则:
,设袋子内有x个白球,则: ![]() ,解得,x=6.
,解得,x=6.
所以袋子内应有6个白球.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场为了吸引顾客,设计了一种促销活动.在一个不透明的箱子里放有4个完全相同的小球,球上分别标有“0元”、“10元”、“30元”和“50元”的字样.规定:顾客在本商场同一日内,消费每满300元,就可以从箱子里先后摸出两个球(每次只摸出一个球,第一次摸出后不放回).商场根据两个小球所标金额之和返还相应价格的购物券,可以重新在本商场消费.某顾客消费刚好满300元,则在本次消费中:
(1)该顾客至少可得元购物券,至多可得元购物券;
(2)请用画树状图或列表法,求出该顾客所获购物券的金额不低于50元的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=30°,以AB为直径的⊙O经过点C.过点C作⊙O的切线交AB的延长线于点P.点D为圆上一点,且
 =
=  ,弦AD的延长线交切线PC于点E,连接BC.
,弦AD的延长线交切线PC于点E,连接BC.
(1)判断OB和BP的数量关系,并说明理由;
(2)若⊙O的半径为2,求AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)
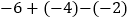 (2)
(2)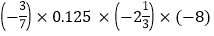
(3)(-2
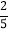 )-(+4.7)-(-0.4)+ (-3.3) (4)
)-(+4.7)-(-0.4)+ (-3.3) (4)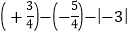
(5)
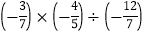 (6)(
(6)( -
- +
+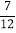 )×(-36)
)×(-36) (7)
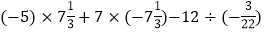 (8)—
(8)—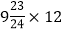 (用简便方法计算)
(用简便方法计算) -
科目: 来源: 题型:
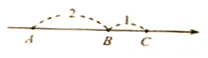
查看答案和解析>>【题目】在一条不完整的数轴上从左到右有点A,B,C,其中AB=2,BC=1,如图所示. 设点A,B,C所对应数的和是p.
(1)若以B为原点,则点A,C所对应的数为 、 ,p的值为 ;若以C为原点,p 的值为 ;
(2)若原点O在图中数轴上点C的右边,且CO=28,求p的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市中小学全面开展“阳光体育”活动,某校在大课间中开设了A(体操)、B(乒乓球)、C(毽球)、D(跳绳)四项活动.为了解学生最喜欢哪一项活动,随机抽取了部分学生进行调查,并将调查结果绘制成了如下两幅不完整的统计图。
请根据统计图回答下列问题:
(1)这次被调查的学生共有_____人;
(2)请将统计图2补充完整;
(3)统计图1中B项目对应的扇形的圆心角是 _____度;
(4)已知该校共有学生1000人,根据调查结果估计该校喜欢体操的学生有_____人.


-
科目: 来源: 题型:
查看答案和解析>>【题目】动点A从原点出发向数轴负方向运动,同时,动点B也从原点出发向数轴正方向运动,运动到3秒钟时,两点相距15个单位长度.已知动点A、B的运动速度比之是3:2(速度单位:1个单位长度/秒).
(1)求两个动点运动的速度;
(2)A、B两点运动到3秒时停止运动,请在数轴上标出此时A、B两点的位置;
(3)若A、B两点分别从(2)中标出的位置再次同时开始在数轴上运动,运动的速度不变,运动的方向不限,问:经过几秒钟,A、B两点之间相距4个单位长度?
相关试题

